题目内容
在等差数列{an}中,a1=2,a17=66,
(1)求数列{an}的通项公式;
(2)88是否是数列{an}中的项.
解:(1)∵由 a1=2,a17=66,可得a17=a1+(17-1)d,
∴d=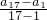 =
=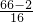 =4,
=4,
∴an=a1 +(n-1)d=2+(n-1)•4=4n-2. …(6分)
(2)令an=88,即4n-2=88得n= ,由于 n∉N+.
,由于 n∉N+.
∴88不是数列{an}中的项.…(12分)
分析:(1)由 a1=2,a17=66,求出公差d 的值,即可得到数列{an}的通项公式.
(2)令an=88,即4n-2=88,解得n值不是正整数,从而得到88不是数列{an}中的项.
点评:本题主要考查等差数列的通项公式的应用,属于基础题.
∴d=
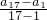 =
=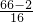 =4,
=4,∴an=a1 +(n-1)d=2+(n-1)•4=4n-2. …(6分)
(2)令an=88,即4n-2=88得n=
 ,由于 n∉N+.
,由于 n∉N+.∴88不是数列{an}中的项.…(12分)
分析:(1)由 a1=2,a17=66,求出公差d 的值,即可得到数列{an}的通项公式.
(2)令an=88,即4n-2=88,解得n值不是正整数,从而得到88不是数列{an}中的项.
点评:本题主要考查等差数列的通项公式的应用,属于基础题.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目