题目内容
【题目】已知圆![]() 的方程为
的方程为![]() ,直线
,直线![]() 的方程为
的方程为![]() ,点
,点![]() 在直线
在直线![]() 上,过点
上,过点![]() 作圆
作圆![]() 的切线
的切线![]() ,切点为
,切点为![]() .
.
(1)若点![]() 的坐标为
的坐标为![]() ,求切线
,求切线![]() 的方程;
的方程;
(2)求四边形![]() 面积的最小值;
面积的最小值;
(3)求证:经过![]() 三点的圆必过定点,并求出所有定点坐标.
三点的圆必过定点,并求出所有定点坐标.
【答案】(1)![]() 或
或![]() (2)
(2)![]() (3)见解析
(3)见解析
【解析】试题分析:(1)解:①当切线斜率不存在时,切线方程为![]() ;②当切线斜率存在时,设切线方程为
;②当切线斜率存在时,设切线方程为![]() ,根据直线和圆相切,求得
,根据直线和圆相切,求得![]() ,即可得到直线的方程;
,即可得到直线的方程;
(2)由四边形![]() 的面积
的面积![]() ,得到当
,得到当![]() 最小时,四边形的面积
最小时,四边形的面积![]() 最小,转化为点到直线的距离,即可求解,即可求解面积的最小值.
最小,转化为点到直线的距离,即可求解,即可求解面积的最小值.
(3)设点![]() ,得到圆心坐标是
,得到圆心坐标是![]() ,进而得到圆的方程,利用圆系方程,进而可判定经过
,进而得到圆的方程,利用圆系方程,进而可判定经过![]() 三点的圆必过定点.
三点的圆必过定点.
试题解析:
(1)①当切线斜率不存在时,切线方程为![]() ;
;
②当切线斜率存在时,设切线方程为![]() ,
,
因为直线和圆相切,所以圆心![]() 到切线的距离
到切线的距离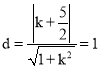 ,解得
,解得![]() ,
,
所以切线方程为![]() ,即
,即![]() .
.
故所求切线方程为![]() 或
或![]() .
.
(2)四边形![]() 的面积
的面积![]() ,
,
所以当![]() 最小时,四边形
最小时,四边形![]() 的面积
的面积![]() 最小.
最小.
又![]() 的最小值是圆心
的最小值是圆心![]() 到直线
到直线![]() 的距离,
的距离,
即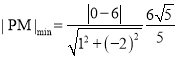 .
.
所以四边形![]() 的面积最小值是
的面积最小值是![]() .
.
(3)证明:过![]() 三点的圆即以
三点的圆即以![]() 为直径的圆,
为直径的圆,
设点![]() ,则圆心坐标是
,则圆心坐标是![]() ,
,
以![]() 为直径的圆的方程是
为直径的圆的方程是![]()
![]() ,
,
化简,得![]() ,
,
即![]() .(*)
.(*)
令![]() ,解得
,解得![]() 或
或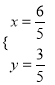 .
.
由于不论![]() 为何值,点
为何值,点![]() 、
、![]() 的坐标都适合方程(*),所以经过
的坐标都适合方程(*),所以经过![]() 三点的圆必过定点,定点坐标是
三点的圆必过定点,定点坐标是![]() 和
和![]() .
.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目



