题目内容
(本小题满分10分)已知双曲线 的两条渐近线均和圆
的两条渐近线均和圆 相切,且双曲线的右焦点为圆
相切,且双曲线的右焦点为圆 的圆心,求该双曲线的方程。
的圆心,求该双曲线的方程。
 的两条渐近线均和圆
的两条渐近线均和圆 相切,且双曲线的右焦点为圆
相切,且双曲线的右焦点为圆 的圆心,求该双曲线的方程。
的圆心,求该双曲线的方程。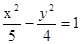
试题分析:把圆
 转化为标准式方程:(x-3)2+y2=4,由此知道圆心C(3,0),圆的半径为2,
转化为标准式方程:(x-3)2+y2=4,由此知道圆心C(3,0),圆的半径为2,因为双曲线
 的右焦点为圆C的圆心,所以a2+b2=9………………①
的右焦点为圆C的圆心,所以a2+b2=9………………①又双曲线的两条渐近线均和圆
 相切,而双曲线的渐近线方程为:bx±ay=0,
相切,而双曲线的渐近线方程为:bx±ay=0,所以
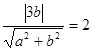 …………………… ②
…………………… ②联立①②得:
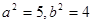 。 所以双曲线的方程:
。 所以双曲线的方程: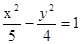 。
。点评:此题重点考查了直线与圆相切的等价条件。主要利用方程的思想进行解题.属于基础题型。

练习册系列答案
相关题目
 ,直线
,直线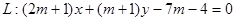
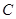 截得的弦长何时最短?并求截得的弦长最短时
截得的弦长何时最短?并求截得的弦长最短时 的值及最短长度。
的值及最短长度。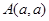 可作圆
可作圆 的两条切线,则实数
的两条切线,则实数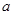 的取值范围为( )
的取值范围为( ) 或
或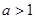
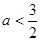
 或
或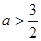
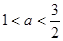
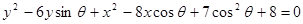 .
.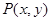 是(1)中曲线C上的动点,求
是(1)中曲线C上的动点,求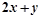 的取值范围.
的取值范围. 的切线,则切线的方程为( )
的切线,则切线的方程为( )

 上一点,直线l与圆O交于A、B两点,
上一点,直线l与圆O交于A、B两点, ,则
,则 面积的最大值为 .
面积的最大值为 . 关于直线2x-y+3=0对称的圆的方程是 ___ .
关于直线2x-y+3=0对称的圆的方程是 ___ .  分成两个弓形当其中劣孤最短时直线
分成两个弓形当其中劣孤最短时直线 的方程为
的方程为