ЬтФПФкШн
ЁОЬтФПЁПЖдгкЪ§Са![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() ЃЌШєТњзу
ЃЌШєТњзу![]() ЃЌдђГЦЪ§Са
ЃЌдђГЦЪ§Са![]() ЮЊЁА
ЮЊЁА![]() Ъ§СаЁБЃЎ
Ъ§СаЁБЃЎ
ШєДцдквЛИіе§ећЪ§![]() ЃЌШєЪ§Са
ЃЌШєЪ§Са![]() жаДцдкСЌајЕФ
жаДцдкСЌајЕФ![]() ЯюКЭИУЪ§СажаСэвЛИіСЌајЕФ
ЯюКЭИУЪ§СажаСэвЛИіСЌајЕФ![]() ЯюЧЁКУАДДЮађЖдгІЯрЕШЃЌдђГЦЪ§Са
ЯюЧЁКУАДДЮађЖдгІЯрЕШЃЌдђГЦЪ§Са![]() ЪЧЁА
ЪЧЁА![]() НзПЩжиИДЪ§СаЁБЃЌ
НзПЩжиИДЪ§СаЁБЃЌ
Р§ШчЪ§Са![]() вђЮЊ
вђЮЊ![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() гы
гы![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() АДДЮађЖдгІЯрЕШЃЌЫљвдЪ§Са
АДДЮађЖдгІЯрЕШЃЌЫљвдЪ§Са![]() ЪЧЁА
ЪЧЁА![]() НзПЩжиИДЪ§СаЁБЃЎ
НзПЩжиИДЪ§СаЁБЃЎ
ЃЈIЃЉЗжБ№ХаЖЯЯТСаЪ§Са![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() ЃЎЪЧЗёЪЧЁА
ЃЎЪЧЗёЪЧЁА![]() НзПЩжиИДЪ§СаЁБЃПШчЙћЪЧЃЌЧыаДГіжиИДЕФет
НзПЩжиИДЪ§СаЁБЃПШчЙћЪЧЃЌЧыаДГіжиИДЕФет![]() ЯюЃЛ
ЯюЃЛ
ЃЈIIЃЉШєЯюЪ§ЮЊ![]() ЕФЪ§Са
ЕФЪ§Са![]() вЛЖЈЪЧ ЁА
вЛЖЈЪЧ ЁА![]() НзПЩжиИДЪ§СаЁБЃЌдђ
НзПЩжиИДЪ§СаЁБЃЌдђ![]() ЕФзюаЁжЕЪЧЖрЩйЃПЫЕУїРэгЩЃЛ
ЕФзюаЁжЕЪЧЖрЩйЃПЫЕУїРэгЩЃЛ
ЃЈIIIЃЉМйЩшЪ§Са![]() ВЛЪЧЁА
ВЛЪЧЁА![]() НзПЩжиИДЪ§СаЁБЃЌШєдкЦфзюКѓвЛЯю
НзПЩжиИДЪ§СаЁБЃЌШєдкЦфзюКѓвЛЯю![]() КѓдйЬэМгвЛЯю
КѓдйЬэМгвЛЯю![]() Лђ
Лђ![]() ЃЌОљПЩ ЪЙаТЪ§СаЪЧЁА
ЃЌОљПЩ ЪЙаТЪ§СаЪЧЁА![]() НзПЩжиИДЪ§СаЁБЃЌЧв
НзПЩжиИДЪ§СаЁБЃЌЧв![]() ЃЌЧѓЪ§Са
ЃЌЧѓЪ§Са![]() ЕФзюКѓвЛЯю
ЕФзюКѓвЛЯю![]() ЕФжЕЃЎ
ЕФжЕЃЎ
ЁОД№АИЁПЃЈIЃЉ![]() ЃЛЃЈЂђЃЉ
ЃЛЃЈЂђЃЉ ![]() ЕФзюаЁжЕЪЧ
ЕФзюаЁжЕЪЧ![]() ЃЛЃЈIIIЃЉ
ЃЛЃЈIIIЃЉ![]() .
.
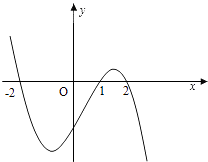
ЁОНтЮіЁПЪдЬтЗжЮіЃКЃЈIЃЉИљОнЬѕМўМАИјГіЕФаТЖЈвхХаЖЯЃЛЃЈIIЃЉНсКЯЫљИјГіЕФаТЖЈвхЃЌЗжРрЬжТлПЩЕУНсЙћЃЛЃЈIIIЃЉгУЗДжЄЗЈНјааЭЦРэЃЌПЩЕУЖј![]() ЁЃ
ЁЃ
ЪдЬтНтЮіЃК
ЃЈIЃЉ![]()
ЃЈЂђЃЉвђЮЊЪ§Са![]() ЕФУПвЛЯюжЛПЩвдЪЧ
ЕФУПвЛЯюжЛПЩвдЪЧ![]() Лђ
Лђ![]() ЃЌЫљвдСЌај
ЃЌЫљвдСЌај![]() ЯюЙВга
ЯюЙВга![]() жжВЛЭЌЕФЧщаЮЃЎ
жжВЛЭЌЕФЧщаЮЃЎ
Шє![]() ЃЌдђЪ§Са
ЃЌдђЪ§Са![]() жага
жага![]() зщСЌај
зщСЌај![]() ЯюЃЌдђетЦфжажСЩйгаСНзщАДДЮађЖдгІЯрЕШЃЌМДЯюЪ§ЮЊ
ЯюЃЌдђетЦфжажСЩйгаСНзщАДДЮађЖдгІЯрЕШЃЌМДЯюЪ§ЮЊ![]() ЕФЪ§Са
ЕФЪ§Са![]() вЛЖЈЪЧЁА
вЛЖЈЪЧЁА![]() НзПЩжиИДЪ§СаЁБЃЛ
НзПЩжиИДЪ§СаЁБЃЛ
Шє![]() ЃЌЪ§Са
ЃЌЪ§Са![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() ВЛЪЧЁА
ВЛЪЧЁА![]() НзПЩжиИДЪ§СаЁБЃЛдђ
НзПЩжиИДЪ§СаЁБЃЛдђ![]() ЪБЃЌОљДцдкВЛЪЧЁА
ЪБЃЌОљДцдкВЛЪЧЁА![]() НзПЩжиИДЪ§СаЁБЕФЪ§Са
НзПЩжиИДЪ§СаЁБЕФЪ§Са![]() ЃЎ
ЃЎ
ЫљвдвЊЪЙЪ§Са![]() вЛЖЈЪЧЁА
вЛЖЈЪЧЁА![]() НзПЩжиИДЪ§СаЁБЃЌдђ
НзПЩжиИДЪ§СаЁБЃЌдђ![]() ЕФзюаЁжЕЪЧ
ЕФзюаЁжЕЪЧ![]() ЃЎ
ЃЎ
ЃЈIIIЃЉгЩгкЪ§Са![]() дкЦфзюКѓвЛЯю
дкЦфзюКѓвЛЯю![]() КѓдйЬэМгвЛЯю
КѓдйЬэМгвЛЯю![]() Лђ
Лђ![]() ЃЌОљПЩЪЙаТЪ§СаЪЧЁА
ЃЌОљПЩЪЙаТЪ§СаЪЧЁА![]() НзПЩжиИДЪ§СаЁБЃЌМДдкЪ§Са
НзПЩжиИДЪ§СаЁБЃЌМДдкЪ§Са![]() ЕФФЉЯю
ЕФФЉЯю![]() КѓдйЬэМгвЛЯю
КѓдйЬэМгвЛЯю![]() Лђ
Лђ![]() ЃЌ
ЃЌ
дђДцдк![]() ЃЌЪЙЕУ
ЃЌЪЙЕУ![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() гы
гы![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() АДДЮађЖдгІЯрЕШЃЌЛђ
АДДЮађЖдгІЯрЕШЃЌЛђ![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() гы
гы![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() АДДЮађЖдгІЯрЕШЃЌШчЙћ
АДДЮађЖдгІЯрЕШЃЌШчЙћ![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() гы
гы![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() ВЛФмАДДЮађЖдгІЯрЕШЃЌ
ВЛФмАДДЮађЖдгІЯрЕШЃЌ
ФЧУДБига![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() ЃЌЪЙЕУ
ЃЌЪЙЕУ![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() ЁЂ
ЁЂ![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() гы
гы![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() АДДЮађЖдгІЯрЕШЃЎ
АДДЮађЖдгІЯрЕШЃЎ
ДЫЪБПМТЧ![]() ЃЌ
ЃЌ ![]() КЭ
КЭ![]() ЃЌЦфжаБигаСНИіЯрЭЌЃЌетОЭЕМжТЪ§Са
ЃЌЦфжаБигаСНИіЯрЭЌЃЌетОЭЕМжТЪ§Са![]() жагаСНИіСЌајЕФЮхЯюЧЁАДДЮађЖдгІЯрЕШЃЌДгЖјЪ§Са
жагаСНИіСЌајЕФЮхЯюЧЁАДДЮађЖдгІЯрЕШЃЌДгЖјЪ§Са![]() ЪЧЁА
ЪЧЁА![]() НзПЩжиИДЪ§СаЁБЃЌетКЭЬтЩшжаЪ§Са
НзПЩжиИДЪ§СаЁБЃЌетКЭЬтЩшжаЪ§Са![]() ВЛЪЧЁА
ВЛЪЧЁА![]() НзПЩжиИДЪ§СаЁБУЌЖмЃЁ
НзПЩжиИДЪ§СаЁБУЌЖмЃЁ
Ыљвд![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() гы
гы![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() АДДЮађЖдгІЯрЕШЃЌДгЖј
АДДЮађЖдгІЯрЕШЃЌДгЖј![]() ЃЎ
ЃЎ