题目内容
某学校拟建一块周长为400m的操场，如图所示，操场的两头是半圆形，中间区域是矩形，学生做操一般安排在矩形区域，为了能让学生的做操区域尽可能大，试问如何设计矩形的长和宽？
100m和
m时，矩形区域面积最大．
m时，矩形区域面积最大．设中间矩形区域的长，宽分别为xm，ym，
中间的矩形区域面积为Sm2，则半圆的周长为
m.
∵操场周长为400m，所以2x＋2×＝400，
即2x＋πy＝400
.
∴S＝xy＝
·(2x)·(πy)≤·
.
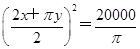由
解得
∴当且仅当时等号成立．
即把矩形的长和宽分别设计为100m和m时，矩形区域面积最大
中间的矩形区域面积为Sm2，则半圆的周长为
m.∵操场周长为400m，所以2x＋2×
＝400，即2x＋πy＝400
.∴S＝xy＝
·(2x)·(πy)≤·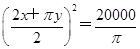.由
解得∴当且仅当
时等号成立．即把矩形的长和宽分别设计为100m和
m时，矩形区域面积最大
练习册系列答案
相关题目
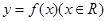满足
且
时，
，函数
分别在两相邻对称轴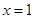
与
处取得最值1与-1，则函数
在区间
内零点的个数为（ ）
，若
时，
恒成立，则实数k的取值范围是 .
的图像是中心对称图形,则
_______.
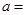)元．
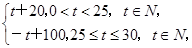且该商品的日销售量Q与时间t(天)的函数关系为Q＝－t＋40(0<t≤30，t∈N)，则这种商品日销量金额最大的一天是30天中的第________天．
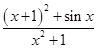的最大值为M,最小值为m,则M+m= .