Question

选修4—1：几何证明选讲

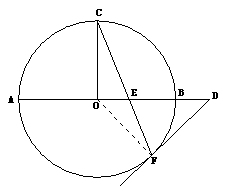
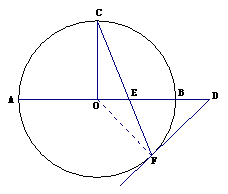
如图，AB是⊙O的直径，C，F是⊙O上的点，OC垂直于直径AB，过F点作⊙O的切线交AB的延长线于D．连结CF交AB于E点.

(1）求证：DE²=DB·DA；

（2）若⊙O的半径为，OB=OE，求EF的长．

Answer 1

选修4—1：几何证明选讲

解:（Ⅰ）连结OF．∵DF切⊙O于F，

∴∠OFD=90°．∴∠OFC+∠CFD=90°．

∵OC=OF，∴∠OCF=∠OFC．

∵CO⊥AB于O，∴∠OCF+∠CEO=90°．

∴∠CFD=∠CEO=∠DEF，∴DF=DE．

∵DF是⊙O的切线,∴DF²=DB·DA．

∴DE²=DB·DA.----------------------------------5分

（Ⅱ），CO=，   ．

∵CE·EF= AE·EB= (+2)(-2)=8，∴EF=2．-----------------------10分