题目内容
 A、选修4-1:几何证明选讲
A、选修4-1:几何证明选讲 如图,PA与⊙O相切于点A,D为PA的中点,
过点D引割线交⊙O于B,C两点,求证:∠DPB=∠DCP.
B.选修4-2:矩阵与变换
已知矩阵M=
|
C.选修4-4:坐标系与参数方程
在极坐标系中,圆C的方程为ρ=2
| 2 |
| π |
| 4 |
|
D.选修4-5:不等式选讲
求函数y=
| 1-x |
| 4+2x |
分析:A 由切割线定理得到 DP2=DA2=DB•DC,即
=
. 因为∠BDP=∠PDC,可得△BDP∽△PDC,从而,∠DPB=∠DCP.
B 写出矩阵M的特征多项式 f(λ),由λ1=3方程f(λ)=0的一根,令x=1 得特征值 λ2=-1,求出它对应的特征向量.
C把参数方程和极坐标方程化为直角坐标方程,求出圆心到直线的距离小于半径,故直线l和⊙C相交.
D y=
+
=(
,
)•(1,
),由|
•
|≤|
| • |
| 求得函数的最大值.
| PD |
| DC |
| DB |
| PD |
B 写出矩阵M的特征多项式 f(λ),由λ1=3方程f(λ)=0的一根,令x=1 得特征值 λ2=-1,求出它对应的特征向量.
C把参数方程和极坐标方程化为直角坐标方程,求出圆心到直线的距离小于半径,故直线l和⊙C相交.
D y=
| 1-x |
| 4+2x |
| 1-x |
| 2+x |
| 2 |
| a |
| b |
| a |
| b |
解答:解:A.因为PA与圆相切于A,所以,DA2=DB•DC,因为D为PA中点,所以,DP=DA,
所以,DP2=DB•DC,即
=
. 因为∠BDP=∠PDC,所以,△BDP∽△PDC,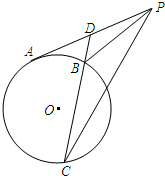
所以,∠DPB=∠DCP.
B.矩阵M的特征多项式为f(λ)=
=(λ-1)(λ-x)-4
因为λ1=3方程f(λ)=0的一根,所以x=1,
由(λ-1)(λ-1)-4=0得λ2=-1,
设λ2=-1对应的一个特征向量为α=
,
则
得 x=-y,令x=1,则y=-1,
所以矩阵M的另一个特征值为-1,对应的一个特征向量为α=
C.消去参数t,得直线l的直角坐标方程为y=2x+1;ρ=2
(sinθ+
)即ρ=2(sinθ+cosθ),
两边同乘以ρ得ρ2=2(ρsinθ+ρcosθ),得⊙C的直角坐标方程为:(x-1)2+(x-1)2=2,
圆心C到直线l的距离d=
=
<
,所以,直线l和⊙C相交.
D.因为y=
+
=(
,
)•(1,
),由|
•
|≤|
| • |
| 求得
∴y的最大值为3,
当且仅当两个向量共线时,即
=
时取“=”号,即当x=0时,ymax=3.
所以,DP2=DB•DC,即
| PD |
| DC |
| DB |
| PD |

所以,∠DPB=∠DCP.
B.矩阵M的特征多项式为f(λ)=
|
因为λ1=3方程f(λ)=0的一根,所以x=1,
由(λ-1)(λ-1)-4=0得λ2=-1,
设λ2=-1对应的一个特征向量为α=
|
则
|
所以矩阵M的另一个特征值为-1,对应的一个特征向量为α=
|
C.消去参数t,得直线l的直角坐标方程为y=2x+1;ρ=2
| 2 |
| π |
| 4 |
两边同乘以ρ得ρ2=2(ρsinθ+ρcosθ),得⊙C的直角坐标方程为:(x-1)2+(x-1)2=2,
圆心C到直线l的距离d=
| |2-1+1| | ||
|
2
| ||
| 5 |
| 2 |
D.因为y=
| 1-x |
| 4+2x |
| 1-x |
| 2+x |
| 2 |
| a |
| b |
| a |
| b |
∴y的最大值为3,
当且仅当两个向量共线时,即
| 1 | ||
|
| ||
|
点评:本题考查简单曲线的极坐标方程,把极坐标方程化为直角坐标方程的方法,直线和圆的位置关系的判定,矩阵的特征值与特征向量的定义.体现了数形结合及转化的数学思想.

练习册系列答案
相关题目
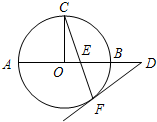 A(选修4-1:几何证明选讲)
A(选修4-1:几何证明选讲) 选做题:在A、B、C、D四小题中只能选做2题,每小题10分,共20分.解答应写出文字说明、证明过程或演算步骤.
选做题:在A、B、C、D四小题中只能选做2题,每小题10分,共20分.解答应写出文字说明、证明过程或演算步骤. A)选修4-1:几何证明选讲
A)选修4-1:几何证明选讲 选做题在A、B、C、D四小题中只能选做2题,每小题10分,共计20分.
选做题在A、B、C、D四小题中只能选做2题,每小题10分,共计20分. 从A,B,C,D四个中选做2个A.选修4-1(几何证明选讲)
从A,B,C,D四个中选做2个A.选修4-1(几何证明选讲)