题目内容
 选修4-1:几何证明选讲
选修4-1:几何证明选讲如图,圆O的直径AB=10,弦DE⊥AB于点H,HB=2.
(1)求DE的长;
(2)延长ED到P,过P作圆O的切线,切点为C,若PC=2
| 5 |
分析:(1)由已知中弦DE⊥AB于点H,AB为圆O的直径,由垂径定理,我们易得DH=HE,进而由相交弦定理,得DH2=AH•BH,由AB=10,,HB=2,代入即可求出DH,进而得到DE的长;
(2)由于PC切圆O于点C,由切割线定理,我们易得PC2=PD•PE,结合(1)的结论和PC=2
,代入即可求出PD的长.
(2)由于PC切圆O于点C,由切割线定理,我们易得PC2=PD•PE,结合(1)的结论和PC=2
| 5 |
解答: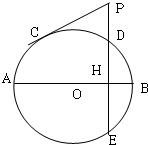 解:(1)∵AB为圆O的直径,AB⊥DE,
解:(1)∵AB为圆O的直径,AB⊥DE,
∴DH=HE,
DH2=AH•BH=(10-2)×2=16,
∴DH=4,
∴DE=8
(2)PC切圆O于点C,
∴PC2=PD•PE,
即(2
)2=PD•(PD+8),
∴PD=2.
 解:(1)∵AB为圆O的直径,AB⊥DE,
解:(1)∵AB为圆O的直径,AB⊥DE,∴DH=HE,
DH2=AH•BH=(10-2)×2=16,
∴DH=4,
∴DE=8
(2)PC切圆O于点C,
∴PC2=PD•PE,
即(2
| 5 |
∴PD=2.
点评:本题考查的知识点是垂径定理,相交弦定理及切割线定理,分析已知线段与未知线段之间的位置关系,进而选择恰当的定义进行求解是解答此类问题的关键.

练习册系列答案
 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案
相关题目
 A、选修4-1:几何证明选讲
A、选修4-1:几何证明选讲  选修4-1:几何证明选讲
选修4-1:几何证明选讲 (2012•徐州模拟)选修4-1:几何证明选讲
(2012•徐州模拟)选修4-1:几何证明选讲 (2013•南京二模)选修4-1:几何证明选讲
(2013•南京二模)选修4-1:几何证明选讲