题目内容
 (2013•南京二模)选修4-1:几何证明选讲
(2013•南京二模)选修4-1:几何证明选讲如图,圆O是等腰三角形ABC的外接圆,AB=AC,延长BC到点D,使得CD=AC,连结AD交圆O于点E,连结BE与AC交于点F,求证:AE2=EF•BE.
分析:等腰△ACD中得∠CAD=∠D,结合圆周角定理证出∠EBC=∠D.等腰△ABC中得到∠ABC=∠ACB,利用△ACD的外角得到∠ACB=∠CAD+∠D=2∠D,从而∠ABC=2∠EBC,所以∠ABE=∠EBC=∠FAE.由∠AEB=∠FEA为两个三角形的公共角,证出△AEB∽△FEA,得到
=
,即得AE2=EF•BE.
| AE |
| FE |
| EB |
| EA |
解答:解:∵△ACD中,CD=AC,∴∠CAD=∠D
∵∠EBC=∠CAD,∴∠EBC=∠D
∵△ABC中,AB=AC,∴∠ABC=∠ACB
∵∠ACB=∠CAD+∠D=2∠D
∴∠ABC=2∠D=2∠EBC,从而∠ABE=∠EBC=∠FAE
又∵∠AEB=∠FEA,∴△AEB∽△FEA
由此可得
=
,即AE2=EF•BE.

∵∠EBC=∠CAD,∴∠EBC=∠D
∵△ABC中,AB=AC,∴∠ABC=∠ACB
∵∠ACB=∠CAD+∠D=2∠D
∴∠ABC=2∠D=2∠EBC,从而∠ABE=∠EBC=∠FAE
又∵∠AEB=∠FEA,∴△AEB∽△FEA
由此可得
| AE |
| FE |
| EB |
| EA |
点评:本题着重考查了圆周角定理、等腰三角形的判定与性质、三角形的外角定理和相似三角形的判定与性质等知识,属于中档题.

练习册系列答案
 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目
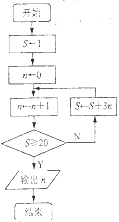 (2013•南京二模)如图是一个算法流程图,其输出的n的值是
(2013•南京二模)如图是一个算法流程图,其输出的n的值是