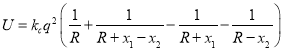题目内容
【题目】设函数![]() .
.
(1)求f(x)的单调区间;
(2)当x>0时,ex﹣ax2﹣x﹣a≥0成立,求正实数a的取值范围.
【答案】(1)单调增区间为![]() ,减区间为
,减区间为![]() (2)
(2)![]()
【解析】
(1)![]() ,令
,令![]() ,得x=1或
,得x=1或![]() ,a>0,即可得出单调性;
,a>0,即可得出单调性;
(2)由ex﹣ax2﹣x﹣a≥0,可得![]() .对a分类讨论,利用(1)的结论即可得出a的取值范围.
.对a分类讨论,利用(1)的结论即可得出a的取值范围.
(1)![]()
令![]() ,得x=1或
,得x=1或![]() ,因为a>0,所以当
,因为a>0,所以当![]() 或x>1时,f'(x)<0;当
或x>1时,f'(x)<0;当![]() 时,f'(x)>0,
时,f'(x)>0,
所以f(x)的单调增区间为![]() ,减区间为
,减区间为![]() ,
,![]() .
.
(2)由ex﹣ax2﹣x﹣a≥0可得![]() .
.
由(1)可知,当![]() ,即0<a≤1时,f(x)在(0,1)单调递增,在(1,+∞)上单调递减,
,即0<a≤1时,f(x)在(0,1)单调递增,在(1,+∞)上单调递减,![]()
依题意有![]() ,即
,即![]() ;
;
当a>1时,![]() ,与题意矛盾.
,与题意矛盾.
所以a的取值范围是![]()

练习册系列答案
相关题目