题目内容
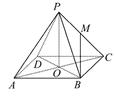
在正四棱锥S－ABCD中，O为顶点在底面上的射影，P为侧棱SD的中点，且SO＝OD，则直线BC与平面PAC所成的角是________．
30°
如图，以O为原点建立空间直角坐标系O－xyz.
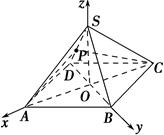
设OD＝SO＝OA＝OB＝OC＝a.则A(a,0,0)，B(0，a,0)，C(－a,0,0)，P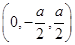
.
则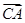
＝(2a,0,0)，
＝
，
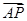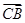＝(a，a,0)，设平面PAC的一个法向量为n，设n＝(x，y，z)，
则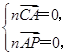
解得
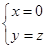可取n＝(0,1,1)，
则cos〈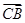，n〉＝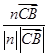
＝
，
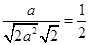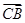∴〈，n〉＝60°，
∴直线BC与平面PAC所成的角为90°－60°＝30°.
设OD＝SO＝OA＝OB＝OC＝a.则A(a,0,0)，B(0，a,0)，C(－a,0,0)，P
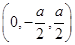.则
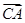＝(2a,0,0)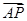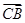，＝，＝(a，a,0)，设平面PAC的一个法向量为n，设n＝(x，y，z)，则
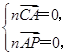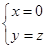解得可取n＝(0,1,1)，则cos〈
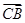，n〉＝＝，∴〈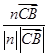
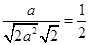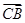，n〉＝60°，∴直线BC与平面PAC所成的角为90°－60°＝30°.
练习册系列答案
名题训练系列答案
期末集结号系列答案
相关题目
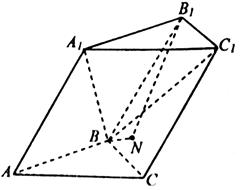
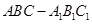中，△ABC是正三角形，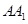
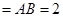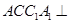，平面
平面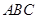
，
.
；
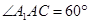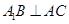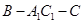的余弦值；
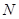是平面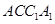
内的动点，求
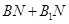的最小值．
=
=
=
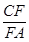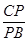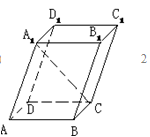
(如图(1)),将△AEF沿EF折起到△
EF的位置,使二面角
EF
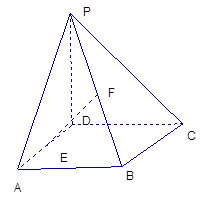
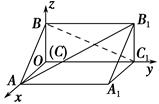
中， AB=1，
，
.
；
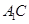—B的余弦值。