题目内容
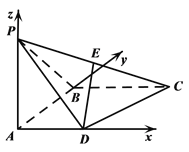
【题目】如图,在四棱锥![]() 中,侧面
中,侧面![]() 底面
底面![]() ,且
,且![]() ,
, ![]() ,
, ![]() ,
, ![]() 是
是![]() 的中点.
的中点.

(Ⅰ)求证: ![]() 平面
平面![]() ;
;
(Ⅱ)求二面角![]() 的余弦值.
的余弦值.
【答案】(Ⅰ)见解析;(Ⅱ) ![]() 。
。
【解析】试题分析:(1)根据条件可得![]() ,
, ![]() 两两垂直,因此可建立空间直角坐标系,然后将
两两垂直,因此可建立空间直角坐标系,然后将![]() 平面
平面![]() 的问题转化成用向量证明
的问题转化成用向量证明![]() ,
, ![]() 的问题;(2)求出平面
的问题;(2)求出平面![]() ,平面
,平面![]() 的法向量,利用两向量的夹角求出二面角的平面角。
的法向量,利用两向量的夹角求出二面角的平面角。
试题解析:
(Ⅰ)证明:因为侧面![]() 底面
底面![]() ,且
,且![]() ,
, ![]() ,
,
所以![]() ,
, ![]() ,
, ![]() ,
,
如图,以点![]() 为坐标原点,分别以直线
为坐标原点,分别以直线![]() ,
, ![]() ,
, ![]() 为
为![]() 轴,
轴, ![]() 轴,
轴, ![]() 轴建立空间直角坐标系.
轴建立空间直角坐标系.
设![]() ,
, ![]() 是
是![]() 的中点,则有
的中点,则有![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
于是![]() ,
, ![]() ,
, ![]() ,
,
因为![]() ,
, ![]() ,
,
所以![]() ,
, ![]() ,且
,且![]() ,
,
因此![]() 平面
平面![]()
(Ⅱ)由(Ⅰ)可知平面![]() 的一个法向量为
的一个法向量为![]() ,
,
设平面![]() 的法向量为
的法向量为![]()
![]() ,
,
![]() ,
, ![]() ,
,
则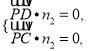 所以
所以![]()
不妨设![]() ,则
,则![]()
![]() ,
,
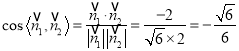 ,
,
由图形知,二面角![]() 为钝角,
为钝角,
所以二面角![]() 的余弦值为
的余弦值为![]() 。
。

【题目】为考察高中生的性别与是否喜欢数学课程之间的关系,在我市某普通中学高中生中随机抽取200名学生,得到如下2×2列联表:
喜欢数学课 | 不喜欢数学课 | 合计 | |
男 | 30 | 60 | 90 |
女 | 20 | 90 | 110 |
合计 | 50 | 150 | 200 |
经计算K2≈6.06,根据独立性检验的基本思想,约有(填百分数)的把握认为“性别与喜欢数学课之间有关系”.
【题目】某公司为确定下一年度投入某种产品的宣传费,需了解年宣传费x(单位:千元)对年销售量y(单位:t)和年利润z(单位:千元)的影响.对近8年的年宣传费xi和年销售量yi(i=1,2,…,8)数据作了初步处理,得到下面的散点图及下面一些统计量的值.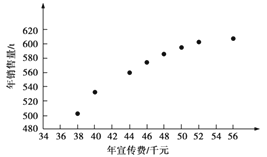
|
|
|
|
|
|
|
46.6 | 563 | 6.8 | 289.8 | 1.6 | 1469 | 108.8 |
表中 ![]() ,
, ![]() .
.
附:对于一组数据(u1,v1),(u2,v2),…,(un,vn),其回归直线v=α+βu的斜率和截距的最下二乘估计分别为 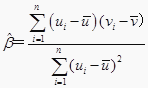 ,
, ![]() .
.
(1)根据散点图判断,y=a+bx与 ![]() 哪一个适宜作为年销售量y关于年宣传费x的回归方程类型?(给出判断即可,不必说明理由)
哪一个适宜作为年销售量y关于年宣传费x的回归方程类型?(给出判断即可,不必说明理由)
(2)根据(1)的判断结果及表中数据,建立y关于x的回归方程;
(3)已知这种产品的年利润z与x,y的关系为z=0.2y-x.根据(2)的结果回答下列问题:
①年宣传费x=49时,年销售量及年利润的预报值时多少?
②年宣传费x为何值时,年利润的预报值最大?
【题目】随着移动互联网的快速发展,基于互联网的共享单车应运而生.某市场研究人员为了了解共享单车运营公司![]() 的经营状况,对该公司最近六个月内的市场占有率进行了统计,并绘制了相应的拆线图.
的经营状况,对该公司最近六个月内的市场占有率进行了统计,并绘制了相应的拆线图.

(1)由拆线图可以看出,可用线性回归模型拟合月度市场占有率![]() 与月份代码
与月份代码![]() 之间的关系.求
之间的关系.求![]() 关于
关于![]() 的线性回归方程,并预测
的线性回归方程,并预测![]() 公司2017年4月份(即
公司2017年4月份(即![]() 时)的市场占有率;
时)的市场占有率;
(2)为进一步扩大市场,公司拟再采购一批单车.现有采购成本分别为1000元/辆和1200元/辆的![]() 两款车型可供选择,按规定每辆单车最多使用4年,但由于多种原因(如骑行频率等)会导致车辆报废年限各不相同.考虑到公司运营的经济效益,该公司决定先对两款车型的单车各100辆进行科学模拟测试,得到两款单车使用寿命频数表如下:
两款车型可供选择,按规定每辆单车最多使用4年,但由于多种原因(如骑行频率等)会导致车辆报废年限各不相同.考虑到公司运营的经济效益,该公司决定先对两款车型的单车各100辆进行科学模拟测试,得到两款单车使用寿命频数表如下:
车型 报废年限 | 1年 | 2年 | 3年 | 4年 | 总计 |
| 20 | 35 | 35 | 10 | 100 |
| 10 | 30 | 40 | 20 | 100 |
经测算,平均每辆单车每年可以带来收入500元.不考虑除采购成本之外的其他成本,假设每辆单车的使用寿命都是整年,且以频率作为每辆单车使用寿命的概率.如果你是![]() 公司的负责人,以每辆单车产生利润的期望值为决策依据,你会选择采购哪款车型?
公司的负责人,以每辆单车产生利润的期望值为决策依据,你会选择采购哪款车型?
(参考公式:回归直线方程为![]() ,其中
,其中 )
)