题目内容
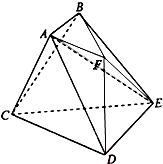 如图,已知多面体ABCDEF中,AB⊥平面ACDF,DE⊥平面ACDF,△ACD是正三角形,且AD=DE=2,AB=AF=1,DF=
如图,已知多面体ABCDEF中,AB⊥平面ACDF,DE⊥平面ACDF,△ACD是正三角形,且AD=DE=2,AB=AF=1,DF=| 3 |
(Ⅰ)求证:DF⊥平面CDE;
(Ⅱ)求多面体ABCDEF的体积.
分析:(1)取△ACD边CD上的中点G,连接AG,由等边三角形三线合一可得AG⊥CD,进而证得四边形AFGD为平行四边形后,可得DF⊥CD,再由DE⊥平面ACDF,由线面垂直的性质可得DE⊥DF,进而由线面垂直的判定定理可得DF⊥平面CDE;
(Ⅱ)将多面体ABCDEF补成一个直三棱柱,则其体积V=VCDE-NFM-VC-ABN-VE-MFB,代入棱柱体积公式及棱锥体积公式,可得答案.
(Ⅱ)将多面体ABCDEF补成一个直三棱柱,则其体积V=VCDE-NFM-VC-ABN-VE-MFB,代入棱柱体积公式及棱锥体积公式,可得答案.
解答:证明: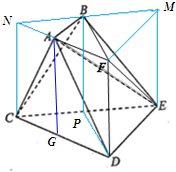 (Ⅰ)∵取△ACD边CD上的中点G,连接AG
(Ⅰ)∵取△ACD边CD上的中点G,连接AG
由△ACD是边长为2的正三角形,
故AG=DF=
,AG⊥CD,DG=AF=1,
则四边形AFGD为平行四边形
则DF⊥CD,
又∵DE⊥平面ACDF,
∴DE⊥DF
又∵DE∩CD=D,DE,CD?平面CDE
∴DF⊥平面CDE.…..…..(6分)
解:(Ⅱ)可证该几何体是直三棱柱EFM-CDE的一部分,
其体积V满足:
…..(12分)
 (Ⅰ)∵取△ACD边CD上的中点G,连接AG
(Ⅰ)∵取△ACD边CD上的中点G,连接AG由△ACD是边长为2的正三角形,
故AG=DF=
| 3 |
则四边形AFGD为平行四边形
则DF⊥CD,
又∵DE⊥平面ACDF,
∴DE⊥DF
又∵DE∩CD=D,DE,CD?平面CDE
∴DF⊥平面CDE.…..…..(6分)
解:(Ⅱ)可证该几何体是直三棱柱EFM-CDE的一部分,
其体积V满足:
|
点评:本题考查的知识点是直线与平面垂直的判定,棱柱,棱锥的体积,熟练掌握线面垂直的性质及判定定理是解答的关键.

练习册系列答案
相关题目
 如图,已知多面体ABCDE中,DE⊥平面DBC,DE∥AB,BD=CD=BC=AB=2,F为BC的中点.
如图,已知多面体ABCDE中,DE⊥平面DBC,DE∥AB,BD=CD=BC=AB=2,F为BC的中点. 如图,已知多面体ABCDE中,AB⊥平面ACD,DE⊥平面ACD,三角形ACD是正三角形,且AD=DE=2,AB=1.
如图,已知多面体ABCDE中,AB⊥平面ACD,DE⊥平面ACD,三角形ACD是正三角形,且AD=DE=2,AB=1. 如图,已知多面体ABCDE中,AB⊥平面ACD,DE⊥平面ACD,AC=AD=CD=DE=2,AB=1,F为CE的中点.
如图,已知多面体ABCDE中,AB⊥平面ACD,DE⊥平面ACD,AC=AD=CD=DE=2,AB=1,F为CE的中点.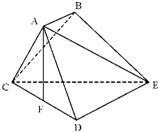 如图,已知多面体ABCDE中,AB⊥平面ACD,DE⊥平面ACD,AC=AD=CD=DE=2,AB=1,F为CD的中点.
如图,已知多面体ABCDE中,AB⊥平面ACD,DE⊥平面ACD,AC=AD=CD=DE=2,AB=1,F为CD的中点.