题目内容
 如图,已知多面体ABCDE中,DE⊥平面DBC,DE∥AB,BD=CD=BC=AB=2,F为BC的中点.
如图,已知多面体ABCDE中,DE⊥平面DBC,DE∥AB,BD=CD=BC=AB=2,F为BC的中点.(Ⅰ)求证:DF⊥平面ABC;
(Ⅱ)求点D到平面EBC的距离的取值范围.
分析:(Ⅰ)利用线面垂直的性质,得到线线垂直,再利用线面垂直的判定,可得DF⊥平面ABC;
(Ⅱ)证明平面DEF⊥平面EBC,连接EF,过D作DH⊥EF,垂足为H,可得线段DH的长即为点D到平面EBC的距离,表示出DH,即可确定其范围.
(Ⅱ)证明平面DEF⊥平面EBC,连接EF,过D作DH⊥EF,垂足为H,可得线段DH的长即为点D到平面EBC的距离,表示出DH,即可确定其范围.
解答:(Ⅰ)证明:∵DE⊥平面DBC,DE∥AB,∴AB⊥平面DBC,
∵DF?平面DBC,∴AB⊥DF
∵BD=CD=BC=2,F为BC的中点
∴DF⊥BC
又∵AB∩BC=B
∴DF⊥平面ABC;
(Ⅱ)解:设DE=x,连接BE,则x>0
∵DE⊥平面DBC,BC?平面DBC,∴DE⊥BC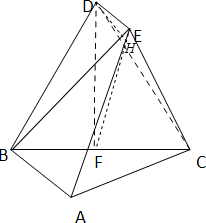
∵DF⊥BC,DE∩DF=D
∴BC⊥平面DEF
∵BC?平面ABC
∴平面DEF⊥平面EBC
连接EF,过D作DH⊥EF,垂足为H,
则DH⊥平面EBC,线段DH的长即为点D到平面EBC的距离
在直角△DEF中,DE=x,DF=
BC=
,∴EF=
∴DH=
=
∈(0,
).
∵DF?平面DBC,∴AB⊥DF
∵BD=CD=BC=2,F为BC的中点
∴DF⊥BC
又∵AB∩BC=B
∴DF⊥平面ABC;
(Ⅱ)解:设DE=x,连接BE,则x>0
∵DE⊥平面DBC,BC?平面DBC,∴DE⊥BC

∵DF⊥BC,DE∩DF=D
∴BC⊥平面DEF
∵BC?平面ABC
∴平面DEF⊥平面EBC
连接EF,过D作DH⊥EF,垂足为H,
则DH⊥平面EBC,线段DH的长即为点D到平面EBC的距离
在直角△DEF中,DE=x,DF=
| ||
| 2 |
| 3 |
| 3+x2 |
∴DH=
| ||
|
| ||||
|
| 3 |
点评:本题考查线面垂直的性质与判定,考查点面距离的计算,属于中档题.

练习册系列答案
相关题目
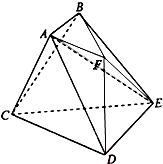 如图,已知多面体ABCDEF中,AB⊥平面ACDF,DE⊥平面ACDF,△ACD是正三角形,且
如图,已知多面体ABCDEF中,AB⊥平面ACDF,DE⊥平面ACDF,△ACD是正三角形,且 如图,已知多面体ABCDE中,AB⊥平面ACD,DE⊥平面ACD,三角形ACD是正三角形,且AD=DE=2,AB=1.
如图,已知多面体ABCDE中,AB⊥平面ACD,DE⊥平面ACD,三角形ACD是正三角形,且AD=DE=2,AB=1. 如图,已知多面体ABCDE中,AB⊥平面ACD,DE⊥平面ACD,AC=AD=CD=DE=2,AB=1,F为CE的中点.
如图,已知多面体ABCDE中,AB⊥平面ACD,DE⊥平面ACD,AC=AD=CD=DE=2,AB=1,F为CE的中点.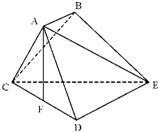 如图,已知多面体ABCDE中,AB⊥平面ACD,DE⊥平面ACD,AC=AD=CD=DE=2,AB=1,F为CD的中点.
如图,已知多面体ABCDE中,AB⊥平面ACD,DE⊥平面ACD,AC=AD=CD=DE=2,AB=1,F为CD的中点.