题目内容
10.已知x∈R,y∈R+,集合A={x2+x+1,-x,-x-1},B={-y,-$\frac{y}{2}$,y+1},若A=B,则x2+y2的值是( )| A. | 5 | B. | 4 | C. | 25 | D. | 10 |
分析 由已知中x∈R,y∈R+,集合A={x2+x+1,-x,-x-1},B={-y,-$\frac{y}{2}$,y+1},A=B,求出满足条件的x,y值,进而可得答案.
解答 解:集合A={x2+x+1,-x,-x-1},B={-y,-$\frac{y}{2}$,y+1},
由x2+x+1>0恒成立,y∈R+得:
x2+x+1=y+1,
则-x-(-x-1)=-$\frac{y}{2}$-(-y)=$\frac{y}{2}$,
即1=$\frac{1}{2}$y,
解得:y=2,
则B={-2,-1,3}
则x=1,A={-2,-1,3}满足条件,
故x2+y2=5,
故选:A.
点评 本题考查的知识点是集合的相等,分类讨论思想,难度中档.

练习册系列答案
 学习实践园地系列答案
学习实践园地系列答案
相关题目
20.已知函数f(x)=3x,f(a+3)=81,函数g(x)=$\frac{{x}^{2}}{x-a}$.
(1)若g(2b)=4,求b的值;
(2)设G(x)=g(x)+g(-x),求G(x)的值域.
(1)若g(2b)=4,求b的值;
(2)设G(x)=g(x)+g(-x),求G(x)的值域.
1.以双曲线$\frac{{x}^{2}}{3}$-$\frac{{y}^{2}}{6}$=1的焦点为顶点,顶点为焦点的椭圆上任意一点P与椭圆的两个焦点构成的三角形的面积的最大值为( )
| A. | 3$\sqrt{6}$ | B. | 3$\sqrt{2}$ | C. | 2$\sqrt{3}$ | D. | 2$\sqrt{2}$ |
18.直线l1:2x+y=0与直线l2:x-y=0的夹角的余弦值为( )
| A. | $\frac{3\sqrt{10}}{10}$ | B. | $\frac{\sqrt{10}}{10}$ | C. | $\frac{\sqrt{5}}{5}$ | D. | $\frac{\sqrt{2}}{2}$ |
9.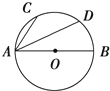 如图,已知AB是圆O的直径,点C、D是半圆弧的两个三等分点,$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{b}$,则$\overrightarrow{AD}$=( )
如图,已知AB是圆O的直径,点C、D是半圆弧的两个三等分点,$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{b}$,则$\overrightarrow{AD}$=( )
 如图,已知AB是圆O的直径,点C、D是半圆弧的两个三等分点,$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{b}$,则$\overrightarrow{AD}$=( )
如图,已知AB是圆O的直径,点C、D是半圆弧的两个三等分点,$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{b}$,则$\overrightarrow{AD}$=( )| A. | $\overrightarrow{a}$-$\frac{1}{2}$$\overrightarrow{b}$ | B. | $\frac{1}{2}$$\overrightarrow{a}$-$\overrightarrow{b}$ | C. | $\overrightarrow{a}$+$\frac{1}{2}$$\overrightarrow{b}$ | D. | $\frac{1}{2}$$\overrightarrow{a}$+$\overrightarrow{b}$ |