题目内容
20.已知函数f(x)=3x,f(a+3)=81,函数g(x)=$\frac{{x}^{2}}{x-a}$.(1)若g(2b)=4,求b的值;
(2)设G(x)=g(x)+g(-x),求G(x)的值域.
分析 (1)由题意得3a+3=81,从而可得g(x)=$\frac{{x}^{2}}{x-1}$,代入解得.
(2)化简G(x)=g(x)+g(-x)=$\frac{{x}^{2}}{x-1}$+$\frac{{x}^{2}}{-x-1}$=x2($\frac{1}{x-1}$-$\frac{1}{x+1}$)=2+$\frac{2}{{x}^{2}-1}$,从而求值域.
解答 解:(1)∵f(x)=3x,f(a+3)=81,
∴3a+3=81,
∴a=1;
∴g(x)=$\frac{{x}^{2}}{x-1}$,
∵g(2b)=4,
∴2b=2,
∴b=1;
(2)G(x)=g(x)+g(-x)
=$\frac{{x}^{2}}{x-1}$+$\frac{{x}^{2}}{-x-1}$=x2($\frac{1}{x-1}$-$\frac{1}{x+1}$)
=2+$\frac{2}{{x}^{2}-1}$,
∵-1≤x2-1,且x2-1≠0,
故$\frac{2}{{x}^{2}-1}$≤-2或$\frac{2}{{x}^{2}-1}$>0;
故2+$\frac{2}{{x}^{2}-1}$≤0或2+$\frac{2}{{x}^{2}-1}$>2;
故G(x)的值域为(-∞,0]∪(2,+∞).
点评 本题考查了函数的应用及函数的值域的求法,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
8.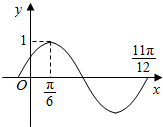 若函数f(x)=sin(ωx+φ)的图象(部分)如图所示,则ω和φ的取值可以是( )
若函数f(x)=sin(ωx+φ)的图象(部分)如图所示,则ω和φ的取值可以是( )
 若函数f(x)=sin(ωx+φ)的图象(部分)如图所示,则ω和φ的取值可以是( )
若函数f(x)=sin(ωx+φ)的图象(部分)如图所示,则ω和φ的取值可以是( )| A. | ω=1,φ=-$\frac{π}{3}$ | B. | ω=2,φ=-$\frac{π}{6}$ | C. | ω=1,φ=$\frac{π}{3}$ | D. | ω=2,φ=$\frac{π}{6}$ |
15.二次函数y=-x2-2x+5,x∈[-2,1]的值域是( )
| A. | [3,6] | B. | [5,6] | C. | [3,5] | D. | [2,6] |
5.函数f(x)=p(x-$\frac{1}{x}$),若f(x)≤$\frac{e}{x}$+lnx在[1,e]上恒成立,则实数p的取值范围是(-∞,$\frac{2e}{{e}^{2}-1}$].
12.数列{an}的通项an=cos2$\frac{nπ}{3}$-sin2$\frac{nπ}{3}$,其前n项和为Sn,则S2015为( )
| A. | -1 | B. | -$\frac{1}{2}$ | C. | 1 | D. | 2 |