题目内容
(本小题满分12分)
已知抛物线C的顶点在 原点,焦点为
原点,焦点为 .
.
(1)求抛物线C的方程;
(2)已知直线 与抛物线C交于
与抛物线C交于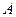 、
、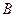 两点,且
两点,且 ,求
,求 的值;
的值;
(3)设点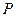 是抛物线C上的动点,点
是抛物线C上的动点,点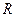 、
、 在
在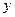 轴上,圆
轴上,圆 内切于
内切于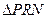 ,求
,求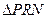 的面积最小值.
的面积最小值.
已知抛物线C的顶点在
 原点,焦点为
原点,焦点为 .
.(1)求抛物线C的方程;
(2)已知直线
 与抛物线C交于
与抛物线C交于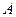 、
、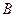 两点,且
两点,且 ,求
,求 的值;
的值;(3)设点
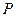 是抛物线C上的动点,点
是抛物线C上的动点,点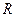 、
、 在
在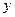 轴上,圆
轴上,圆 内切于
内切于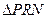 ,求
,求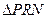 的面积最小值.
的面积最小值.解:(1)设抛物线C的方程为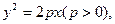
由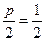 ,即
,即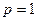 ,
,
所以抛物线C的方程 为
为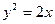 …………4分
…………4分
(2)设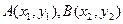 ,由
,由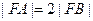
得故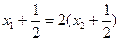
即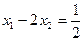 ①
①
又由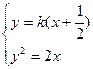 得
得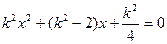
故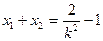 ②
②
 ③
③
解①②③构成的方程组得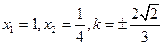
又由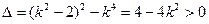 ,即
,即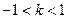 ,所求得的
,所求得的 适合,
适合,
因此所求得的 的值为
的值为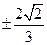 …………9分
…………9分
(3)设 ,且
,且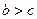
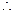 直线PR的方程为
直线PR的方程为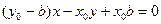
 圆
圆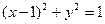 内切于
内切于 ,
,
由则圆心(1,0)到直线PR的距离为1,
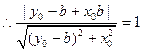 化简得
化简得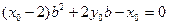
同 理可得
理可得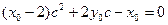
由于 ,所以
,所以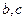 为方程
为方程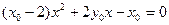 的两根,
的两根,
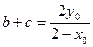 ,
,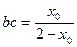 ,
,
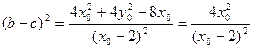
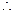
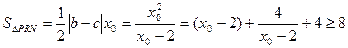 ,
,
当且仅当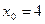 时取等号,
时取等号,
所以 的面积最小值为
的面积最小值为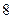 . …(15分)
. …(15分)
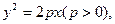
由
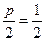 ,即
,即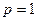 ,
, 所以抛物线C的方程
 为
为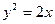 …………4分
…………4分(2)设
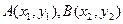 ,由
,由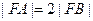
得故
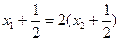
即
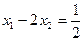 ①
①又由
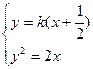 得
得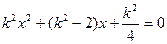
故
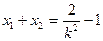 ②
② ③
③解①②③构成的方程组得
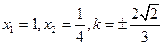
又由
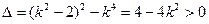 ,即
,即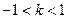 ,所求得的
,所求得的 适合,
适合,因此所求得的
 的值为
的值为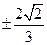 …………9分
…………9分(3)设
 ,且
,且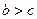
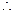 直线PR的方程为
直线PR的方程为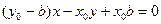
 圆
圆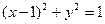 内切于
内切于 ,
,由则圆心(1,0)到直线PR的距离为1,
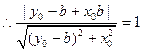 化简得
化简得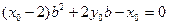
同
 理可得
理可得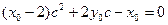
由于
 ,所以
,所以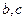 为方程
为方程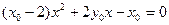 的两根,
的两根,
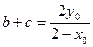 ,
,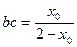 ,
,
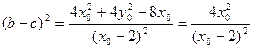
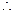
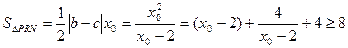 ,
,当且仅当
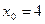 时取等号,
时取等号,所以
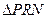 的面积最小值为
的面积最小值为 . …(15分)
. …(15分)略

练习册系列答案
相关题目
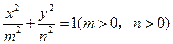 的右焦点与抛物线
的右焦点与抛物线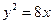 的焦点相同,离心率为
的焦点相同,离心率为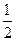 ,则此椭圆的方程为( )
,则此椭圆的方程为( )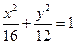
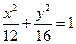
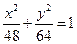
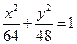
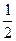 )为方向向量的直线l过点(0,
)为方向向量的直线l过点(0, 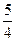 ),抛物线C:
),抛物线C: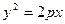 (p>0)的顶点关于直线l的对称点在该抛物的准线上.
(p>0)的顶点关于直线l的对称点在该抛物的准线上.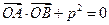 (O为原点,A、B异于原点),试求点N的轨迹方程.
(O为原点,A、B异于原点),试求点N的轨迹方程.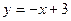 与
与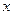 轴、
轴、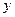 轴分别交于
轴分别交于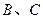 ,抛物线
,抛物线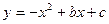 经过点
经过点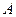 是抛物线与
是抛物线与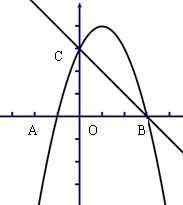
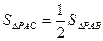 ,求P点坐标。
,求P点坐标。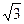 ,则M到该抛物线焦点的距离为
,则M到该抛物线焦点的距离为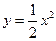 (
(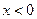 )上,并且与抛物线的准线及y轴都相切的圆的方程是_
)上,并且与抛物线的准线及y轴都相切的圆的方程是_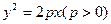 焦点为F,准线为l,经过F的直线与抛物线交于A、B两点,交准线于C点,点A在x轴上方,AK⊥l,垂足为K,若|BC|=2|BF|,且|AF|=4,则△AKF的面积是 ( )
焦点为F,准线为l,经过F的直线与抛物线交于A、B两点,交准线于C点,点A在x轴上方,AK⊥l,垂足为K,若|BC|=2|BF|,且|AF|=4,则△AKF的面积是 ( )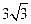 C.
C.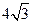 D.8
D.8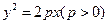 的准线与圆
的准线与圆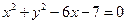 相切,则
相切,则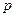 的值为 .
的值为 .