题目内容
【题目】已知函数f(x)=2lnx﹣x.
(I)写出函数f(x)的定义域,并求其单调区间;
(II)已知曲线y=f(x)在点(x0,f(x0))处的切线为l,且l在y轴上的截距是﹣2,求x0.
【答案】(Ⅰ)定义域为(0,+∞), 单调递增区间是(0,2),单调递减区间是(2,+∞);(Ⅱ)1.
【解析】
(Ⅰ)由对数真数大于零求得函数的定义域,利用导数求得函数的单调区间.(Ⅱ)利用切点的横坐标求得斜率,由点斜式写出切线方程,令纵截距为![]() 列方程,解方程求得
列方程,解方程求得![]() 的值.
的值.
解:(Ⅰ)函数y=f(x)的定义域为:(0,+∞).
∵f(x)=2lnx﹣x,∴![]() .
.
令f'(x)=0,则x=2.
当x在(0,+∞)上变化时,f'(x),f(x)的变化情况如下表
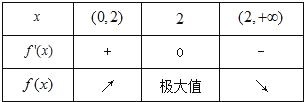
∴函数y=f(x)的单调递增区间是(0,2),单调递减区间是(2,+∞).
(Ⅱ)由题意可知:f(x0)=2lnx0﹣x0,
曲线y=f(x)在点(x0,f(x0))处的切线的斜率为![]() .
.
∴切线方程为:![]() .
.
∴![]() .
.
∴![]() .
.
∵切线方程为y=kx﹣2,
∴2lnx0﹣2=﹣2.
∴x0=1.

练习册系列答案
相关题目
【题目】某公司准备将![]() 万元资金投入到市环保工程建设中,现有甲、乙两个建设项目选择,若投资甲项目一年后可获得的利润
万元资金投入到市环保工程建设中,现有甲、乙两个建设项目选择,若投资甲项目一年后可获得的利润![]() (万元)的概率分布列如表所示:
(万元)的概率分布列如表所示:
|
|
|
|
|
|
|
|
且![]() 的期望
的期望![]() ;若投资乙项目一年后可获得的利润
;若投资乙项目一年后可获得的利润![]() (万元)与该项目建设材料的成本有关,在生产的过程中,公司将根据成本情况决定是否在第二和第三季度进行产品的价格调整,两次调整相互独立且调整的概率分别为
(万元)与该项目建设材料的成本有关,在生产的过程中,公司将根据成本情况决定是否在第二和第三季度进行产品的价格调整,两次调整相互独立且调整的概率分别为![]() 和
和![]() .若乙项目产品价格一年内调整的次数
.若乙项目产品价格一年内调整的次数![]() (次数)与
(次数)与![]() 的关系如表所示:
的关系如表所示:
|
|
|
|
|
|
|
|
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)求![]() 的分布列;
的分布列;
(Ⅲ)若该公司投资乙项目一年后能获得较多的利润,求![]() 的取值范围.
的取值范围.