题目内容
3.已知向量$\overrightarrow{a}$=(1,$\sqrt{3}$),$\overrightarrow{b}$=(-2,0).点O是坐标原点.(1)设$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,若四边形OACB是平行四边形,求点C的坐标;
(2)若$\overrightarrow{a}$+$\overrightarrow{b}$+$\overrightarrow{c}$=0,求证$\overrightarrow{c}$⊥($\overrightarrow{a}$-$\overrightarrow{b}$);
(3)求<$\overrightarrow{a}$-$\overrightarrow{b}$,$\overrightarrow{a}$>的值;
(4)若$\overrightarrow{c}$$⊥\overrightarrow{b}$($\overrightarrow{c}$≠$\overrightarrow{0}$),当t∈[-$\sqrt{3}$,2]时,求|$\overrightarrow{a}$-t$\frac{\overrightarrow{c}}{|\overrightarrow{c}|}$|的取值范围;
(5)若|$\overrightarrow{c}$|=|$\overrightarrow{a}$|,求($\overrightarrow{a}$+$\overrightarrow{b}$+$\overrightarrow{c}$)•$\overrightarrow{c}$的最大值及<$\overrightarrow{c}$-$\frac{\overrightarrow{b}}{2}$,$\overrightarrow{c}$>的最大值.
分析 (1)由向量加法的平行四边形法则,可得$\overrightarrow{OC}$=$\overrightarrow{OA}$+$\overrightarrow{OB}$,即可得到所求;
(2)运用向量垂直的条件:数量积为0,即可得证;
(3)运用向量的夹角公式,计算即可得到;
(4)设$\overrightarrow{c}$=(x,y),即有-2x=0,即x=0,y≠0,再由向量的平方即为模的平方,讨论y>0,y<0,即可得到t的二次函数,求得最值,即可得到所求范围;
(5)运用向量的几何意义,通过圆的知识,即可得到($\overrightarrow{a}$+$\overrightarrow{b}$+$\overrightarrow{c}$)•$\overrightarrow{c}$的最大值,再由余弦定理,结合基本不等式即可得到<$\overrightarrow{c}$-$\frac{\overrightarrow{b}}{2}$,$\overrightarrow{c}$>的最大值.
解答 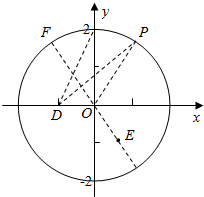 解:(1)设$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,若四边形OACB是平行四边形,
解:(1)设$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,若四边形OACB是平行四边形,
则$\overrightarrow{OC}$=$\overrightarrow{OA}$+$\overrightarrow{OB}$=(1,$\sqrt{3}$)+(-2,0)=(-1,$\sqrt{3}$),即有C(-1,$\sqrt{3}$);
(2)证明:若$\overrightarrow{a}$+$\overrightarrow{b}$+$\overrightarrow{c}$=0,则$\overrightarrow{c}$=-($\overrightarrow{a}$+$\overrightarrow{b}$),
即有$\overrightarrow{c}$•($\overrightarrow{a}$-$\overrightarrow{b}$)=-($\overrightarrow{a}$+$\overrightarrow{b}$)•($\overrightarrow{a}$-$\overrightarrow{b}$)=-($\overrightarrow{a}$2-$\overrightarrow{b}$2)=-(4-4)=0,
则$\overrightarrow{c}$⊥($\overrightarrow{a}$-$\overrightarrow{b}$);
(3)cos<$\overrightarrow{a}$-$\overrightarrow{b}$,$\overrightarrow{a}$>=$\frac{(\overrightarrow{a}-\overrightarrow{b})•\overrightarrow{a}}{|\overrightarrow{a}-\overrightarrow{b}|•|\overrightarrow{a}|}$=$\frac{{\overrightarrow{a}}^{2}-\overrightarrow{a}•\overrightarrow{b}}{\sqrt{9+3}•2}$=$\frac{4+2}{4\sqrt{3}}$=$\frac{\sqrt{3}}{2}$,
由0≤<$\overrightarrow{a}$-$\overrightarrow{b}$,$\overrightarrow{a}$>≤π,可得<$\overrightarrow{a}$-$\overrightarrow{b}$,$\overrightarrow{a}$>=$\frac{π}{6}$;
(4)若$\overrightarrow{c}$$⊥\overrightarrow{b}$($\overrightarrow{c}$≠0),则$\overrightarrow{c}$•$\overrightarrow{b}$=0,
设$\overrightarrow{c}$=(x,y),即有-2x=0,即x=0,y≠0,
则f(t)=|$\overrightarrow{a}$-t$\frac{\overrightarrow{c}}{|\overrightarrow{c}|}$|2=$\overrightarrow{a}$2-$\frac{2t\overrightarrow{a}•\overrightarrow{c}}{|\overrightarrow{c}|}$+t2
=t2+4-$\frac{2\sqrt{3}y}{|y|}$t,当y>0时,f(t)=t2+4-2$\sqrt{3}$t,
由t∈[-$\sqrt{3}$,2],可得f(t)∈[1,13];
当y<0时,f(t)=t2+4+2$\sqrt{3}$t,
由t∈[-$\sqrt{3}$,2],可得f(t)∈[13,8+4$\sqrt{3}$].
即有f(t)∈[1,8+4$\sqrt{3}$],
则|a-t$\frac{\overrightarrow{c}}{|\overrightarrow{c}|}$|的取值范围为[1,$\sqrt{2}$+$\sqrt{6}$];
(5)|$\overrightarrow{c}$|=|$\overrightarrow{a}$|=2,设$\overrightarrow{c}$=(m,n),即有m2+n2=4,
即为以O为圆心,2为半径的圆,
($\overrightarrow{a}$+$\overrightarrow{b}$+$\overrightarrow{c}$)•$\overrightarrow{c}$=m(m-1)+n(n+$\sqrt{3}$)=(m-$\frac{1}{2}$)2+(n+$\frac{\sqrt{3}}{2}$)2-1,
即为点(m,n)与($\frac{1}{2}$,-$\frac{\sqrt{3}}{2}$)的距离的平方减去1,
连接圆心和(($\frac{1}{2}$,-$\frac{\sqrt{3}}{2}$)延长与圆相交,可得F即为所求.
则有($\overrightarrow{a}$+$\overrightarrow{b}$+$\overrightarrow{c}$)•$\overrightarrow{c}$的最大值为(2+$\sqrt{\frac{1}{4}+\frac{3}{4}}$)2-1=8;
又$\overrightarrow{OD}$=(-1,0)=$\frac{1}{2}$$\overrightarrow{b}$,<$\overrightarrow{c}$-$\frac{\overrightarrow{b}}{2}$,$\overrightarrow{c}$>=<$\overrightarrow{DP}$,$\overrightarrow{OP}$>=∠OPD,
设PD=x,由余弦定理可得cos∠OPD=$\frac{4+{x}^{2}-1}{4x}$=$\frac{1}{4}$(x+$\frac{3}{x}$)≥$\frac{1}{4}$×2$\sqrt{3}$=$\frac{\sqrt{3}}{2}$,
当且仅当x=$\sqrt{3}$<2,取得等号.
可得∠OPD≤$\frac{π}{6}$,即有<$\overrightarrow{c}$-$\frac{\overrightarrow{b}}{2}$,$\overrightarrow{c}$>的最大值为$\frac{π}{6}$.
点评 本题考查向量的数量积的坐标运算,考查向量垂直的条件和夹角的大小和最值的求法,同时考查函数的思想和数形结合的思想方法,属于综合题.

 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案| A. | 4(3$\sqrt{3}$+4) | B. | 8(2$\sqrt{3}$+1) | C. | 12(2$\sqrt{3}$+1) | D. | 3($\sqrt{3}$+8) |
 某算法的流程图如图所示,记输出的数组(x,y)依次为(x1,y1),(x2,y2),…(x3,y3)…,若程序运行中输出的一个数组是(9,y),则y=-4;程序结束时,共输出(x,y)的组数为1008.
某算法的流程图如图所示,记输出的数组(x,y)依次为(x1,y1),(x2,y2),…(x3,y3)…,若程序运行中输出的一个数组是(9,y),则y=-4;程序结束时,共输出(x,y)的组数为1008.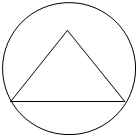 棱长为3的正四面体的四个顶点都在同一个球面上,若过该球球心的一个截面如图,求图中三角形的面积、该球的表面积和体积.
棱长为3的正四面体的四个顶点都在同一个球面上,若过该球球心的一个截面如图,求图中三角形的面积、该球的表面积和体积.