题目内容
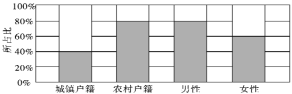
【题目】为推动实施健康中国战略,树立国家大卫生、大健康概念,手机APP也推出了多款健康运动软件,如“微信运动”,杨老师的微信朋友圈内有![]() 位好友参与了“微信运动”,他随机选取了
位好友参与了“微信运动”,他随机选取了![]() 位微信好友(女
位微信好友(女![]() 人,男
人,男![]() 人),统计其在某一天的走路步数,其中,女性好友的走路步数数据记录如下:
人),统计其在某一天的走路步数,其中,女性好友的走路步数数据记录如下:
5860 | 8520 | 7326 | 6798 | 7325 | 8430 | 3216 | 7453 | 11754 | 9860 |
8753 | 6450 | 7290 | 4850 | 10223 | 9763 | 7988 | 9176 | 6421 | 5980 |
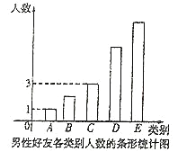
男性好友走路的步数情况可分为五个类别:![]() 步(说明“
步(说明“![]() ”表示大于等于
”表示大于等于![]() ,小于等于
,小于等于![]() ,下同),
,下同),![]() 步,
步,![]() 步,
步,![]() 步及以上,且
步及以上,且![]() 三种类别人数比例为
三种类别人数比例为![]() ,将统计结果绘制如图所示的条形图,若某人一天的走路步数超过
,将统计结果绘制如图所示的条形图,若某人一天的走路步数超过![]() 步被系统认定为“卫健型”,否则被系统认定为“进步型”.
步被系统认定为“卫健型”,否则被系统认定为“进步型”.
(1)若以杨老师选取的好友当天行走步数的频率分布来估计所有微信好友每日走路步数的概率分布,请估计杨老师的微信好友圈里参与“微信运动”的![]() 名好友中,每天走路步数在
名好友中,每天走路步数在![]() 步的人数;
步的人数;
(2)请根据选取的样本数据完成下面的![]() 列联表并据此判断能否有
列联表并据此判断能否有![]() 以上的把握认定“认定类型”与“性别”有关?
以上的把握认定“认定类型”与“性别”有关?
卫健型 | 进步型 | 总计 | |
男 | 20 | ||
女 | 20 | ||
总计 | 40 |
附: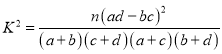 ,
,
| 0.10 | 0.05 | 0.025 | 0.010 |
| 2.706 | 3.841 | 5.024 | 6.635 |
【答案】(1)375
(2)列联表见解析,没有![]() 以上的把握认定“认定类型”与“性别”有关
以上的把握认定“认定类型”与“性别”有关
【解析】
(1)由条形统计图,男性朋友![]() 类型设为
类型设为![]() ,由总人数为20人,得到各个类型的人数,由此得出每天走路步数在
,由总人数为20人,得到各个类型的人数,由此得出每天走路步数在![]() 步的人数,由此得到600人时符合题意的人数;
步的人数,由此得到600人时符合题意的人数;
(2)根据题设所给数据填写![]() 列联表,再计算
列联表,再计算![]() ,对照题设中的表格,得出统计结论.
,对照题设中的表格,得出统计结论.
解:(1)在样本数据中,男性朋友![]() 类型设为
类型设为![]() ,
,
则由题意知![]() ,可得
,可得![]() ,
,
即![]() 类型有
类型有![]() 人,
人,![]() 类型有
类型有![]() 人,
人,![]() 类型有
类型有![]() 人,
人,
则男性朋友走路步数在![]() 步的包括
步的包括![]() 两类型共计
两类型共计![]() 人;
人;
又女性朋友走路步数在![]() 步的共计16人;
步的共计16人;
则用样本数据估计所有微信好友每天走路步数在![]() 步的人数为
步的人数为![]() ;
;
(2)根据题意在抽取的40个样本数据的![]() 列联表如下:
列联表如下:
卫健型 | 进步型 | 总计 | |
男 | 14 | 6 | 20 |
女 | 8 | 12 | 20 |
总计 | 22 | 18 | 40 |
由![]() 列联表可得
列联表可得![]() ,
,
故没有![]() 以上的把握认定“认定类型”与“性别”有关.
以上的把握认定“认定类型”与“性别”有关.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】某地区高考实行新方案,规定:语文、数学和英语是学生的必考科目,学生还须从物理、化学、生物、历史、地理和政治六个科目中选取三个科目作为选考科目.若一个学生从六个科目中选出了三个科目作为选考科目,则称该学生确定选考方案,否则称该学生待确定选考方案.例如学生甲选择“物理、化学和生物”三个选考科目,则称学生甲确定选考方案.某校为了解高一年级![]() 名学生选考科目的意向,随机选取
名学生选考科目的意向,随机选取![]() 名学生进行了一次调查,统计情况如下表:
名学生进行了一次调查,统计情况如下表:
性别 | 选考方案确定情况 | 物理 | 化学 | 生物 | 历史 | 地理 | 政治 |
男 生 | 选考方案确定的有 |
|
|
|
|
|
|
选考方案待确定的有 |
|
|
|
|
|
| |
女 生 | 选考方案确定的有 |
|
|
|
|
|
|
选考方案待确定的有 |
|
|
|
|
|
|
(1)估计该校高一年级已确定选考方案的学生有多少人?
(2)假设男生、女生选择选考科目是相互独立的.从确定选考方案的![]() 名男生中随机选出
名男生中随机选出![]() 名,从确定选考方案的
名,从确定选考方案的![]() 名女生中随机选出
名女生中随机选出![]() 名,试求该男生和该女生的选考方案中都含有历史科目的概率;
名,试求该男生和该女生的选考方案中都含有历史科目的概率;
(3)从确定选考方案的8名男生中随机选出2名,设随机变量![]() 表示
表示![]() 名男生选考方案相同,
名男生选考方案相同,![]() 表示
表示![]() 名男生选考方案不同,求
名男生选考方案不同,求![]() 的分布列及数学期望.
的分布列及数学期望.