Question

【题目】已知为椭圆的左、右焦点，点在椭圆上移动时， 的内心的轨迹方程为__________．

Answer 1

【答案】

【解析】考查更为一般的问题：设P为椭圆C: 上的动点， 为椭圆的两个焦点， 为△PF1F2的内心，求点I的轨迹方程．

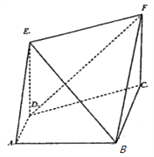
解法一：如图，设内切圆I与F1F2的切点为H，半径为r，且F1H=y，F2H=z，PF1=x+y，PF2=x+z， ，则.

直线IF1与IF2的斜率之积： ，

而根据海伦公式，有△PF1F2的面积为

因此有.

再根据椭圆的斜率积定义，可得I点的轨迹是以F1F2为长轴，

离心率e满足的椭圆，

其标准方程为.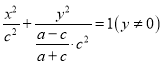

解法二：令，则．三角形PF1F2的面积：

，

其中r为内切圆的半径，解得.

另一方面，由内切圆的性质及焦半径公式得：

从而有．消去θ得到点I的轨迹方程为：

.

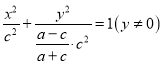本题中： ，代入上式可得轨迹方程为： .