题目内容
已知椭圆
+
=1(a>b>0)的左焦点为F1(-1,0),离心率为
.
(1)求椭圆的标准方程;
(2)设过点F且不与坐标轴垂直的直线l交椭圆于A,B两点,线段AB的垂直平分线与x轴交于点G,求点G的横坐标的取值范围.
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
(1)求椭圆的标准方程;
(2)设过点F且不与坐标轴垂直的直线l交椭圆于A,B两点,线段AB的垂直平分线与x轴交于点G,求点G的横坐标的取值范围.
分析:(1)利用椭圆的离心率的定义求出a,利用椭圆中三个参数的关系求出b2=1,写出椭圆的方程.
(2)欲求点G横坐标的取值范围,从函数思想的角度考虑,先将其表示成某一变量的函数,后求函数的值域,这里取直线AB的斜率K为自变量,通过解方程组求得点G横坐标(用k表示),再求其取值范围.
(2)欲求点G横坐标的取值范围,从函数思想的角度考虑,先将其表示成某一变量的函数,后求函数的值域,这里取直线AB的斜率K为自变量,通过解方程组求得点G横坐标(用k表示),再求其取值范围.
解答: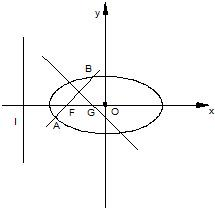 解:(1)因为椭圆
解:(1)因为椭圆
+
=1(a>b>0)的左焦点为F1(-1,0),
所以c=1,
又因为离心率为
,
所以a=
所以b2=1
所以椭圆的方程为
+y2=1,
(2)设直线AB的方程为y=k(x+1)(k≠0),
代入
+y2=1,整理得
(1+2k2)x2+4k2x+2k2-2=0.
∵直线AB过椭圆的左焦点F,
∴方程有两个不等实根.
记A(x1,y1),B(x2,y2),AB中点N(x0,y0),
则 x1+x2=-
,
∴AB的垂直平分线NG的方程为 y-y0=-
(x-x0).
令y=0,得 xG=x0+ky0=-
+
=-
=-
+
.
∵k≠0,∴-
<xG<0,
∴点G横坐标的取值范围为 (-
,0).
 解:(1)因为椭圆
解:(1)因为椭圆| x2 |
| a2 |
| y2 |
| b2 |
所以c=1,
又因为离心率为
| ||
| 2 |
所以a=
| 2 |
所以b2=1
所以椭圆的方程为
| x2 |
| 2 |
(2)设直线AB的方程为y=k(x+1)(k≠0),
代入
| x2 |
| 2 |
(1+2k2)x2+4k2x+2k2-2=0.
∵直线AB过椭圆的左焦点F,
∴方程有两个不等实根.
记A(x1,y1),B(x2,y2),AB中点N(x0,y0),
则 x1+x2=-
| 4k2 |
| 2k2+1 |
∴AB的垂直平分线NG的方程为 y-y0=-
| 1 |
| k |
令y=0,得 xG=x0+ky0=-
| 2k2 |
| 2k2+1 |
| k2 |
| 2k2+1 |
| k2 |
| 2k2+1 |
| 1 |
| 2 |
| 1 |
| 4k2+2 |
∵k≠0,∴-
| 1 |
| 2 |
∴点G横坐标的取值范围为 (-
| 1 |
| 2 |
点评:本小题主要考查直线、圆、椭圆和不等式等基本知识,考查平面解析几何的基本方法,考查运算能力和综合解题能力,直线与圆锥曲线的位置关系问题,通常是先联立组成方程组,消去x(或y),得到y(或x)的方程.我们在研究圆锥曲线时,经常涉及到直线与圆锥曲线的位置关系的研究.主要涉及到:交点问题、弦长问题、弦中点(中点弦)等问题,常用的方法:联立方程组,借助于判别式,数形结合法等.

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目