题目内容
已知椭圆
+
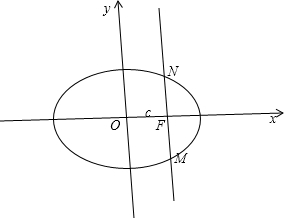
=1（a＞b＞0）的右焦点为F，过F作y轴的平行线交椭圆于M、N两点，若|MN|=3，且椭圆离心率是方程2x2-5x+2=0的根，求椭圆方程．
| x2 |
| a2 |
| y2 |
| b2 |
分析：把x=c代入
+
=1中，得y2=
，∴y=±
．∴|MN|=
=3．再根据a2=b2+c2椭圆离心率e=
，求得a、b，从而求得椭圆的方程．
| x2 |
| a2 |
| y2 |
| b2 |
| b4 |
| a2 |
| b2 |
| a |
| 2b2 |
| a |
| c |
| a |
解答：解：∵右焦点为F（c，0），把x=c代入
+
=1中，得y2=
，
∴y=±
．∴|MN|=
=3．①
又2x2-5x+2=0⇒（2x-1）（x-2）=0，∴x=
或2，
又e∈（0，1），∴e=
，即
=
．②
又知a2=b2+c2，③
由①②③联立解得a=2，b=
，c=1，
∴椭圆方程为
+
=1．
| x2 |
| a2 |
| y2 |
| b2 |
| b4 |
| a2 |
∴y=±
| b2 |
| a |
| 2b2 |
| a |
又2x2-5x+2=0⇒（2x-1）（x-2）=0，∴x=
| 1 |
| 2 |
又e∈（0，1），∴e=
| 1 |
| 2 |
| c |
| a |
| 1 |
| 2 |
又知a2=b2+c2，③
由①②③联立解得a=2，b=
| 3 |
∴椭圆方程为
| x2 |
| 4 |
| y2 |
| 3 |
点评：本题考查了椭圆的简单几何性质，椭圆的标准方程，解题的关键是用a，b表示|MN|．
练习册系列答案
小学课堂作业系列答案
金博士一点全通系列答案
相关题目