题目内容
如图,在 ABC中,
ABC中, C=90°,AC="b," BC="a," P为三角形内的一点,且
C=90°,AC="b," BC="a," P为三角形内的一点,且 ,
,
(Ⅰ)建立适当的坐标系求出P的坐标;
(Ⅱ)求证:│PA│2+│PB│2=5│PC│2
(Ⅲ)若a+2b=2,求以PA,PB,PC分别为直径的三个圆的面积之和的最小值,并求出此时的b值.
 ABC中,
ABC中, C=90°,AC="b," BC="a," P为三角形内的一点,且
C=90°,AC="b," BC="a," P为三角形内的一点,且 ,
,(Ⅰ)建立适当的坐标系求出P的坐标;
(Ⅱ)求证:│PA│2+│PB│2=5│PC│2
(Ⅲ)若a+2b=2,求以PA,PB,PC分别为直径的三个圆的面积之和的最小值,并求出此时的b值.

以边CA、CB所在直线分别为x轴、y轴建立直角坐标系,,设A(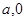 )、B(0,b),P点的坐标为(x,y),由条件可知
)、B(0,b),P点的坐标为(x,y),由条件可知 =
=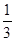
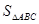 ,可求出x=
,可求出x=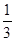
 ,y=
,y=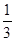 b,再分别用两点距离公式即可,(3)将a=2-2b代入s的表达式,得到b的一个二次函数.
b,再分别用两点距离公式即可,(3)将a=2-2b代入s的表达式,得到b的一个二次函数.
当b=0.8时,s最小.
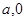 )、B(0,b),P点的坐标为(x,y),由条件可知
)、B(0,b),P点的坐标为(x,y),由条件可知 =
=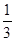
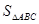 ,可求出x=
,可求出x=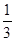
 ,y=
,y=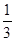 b,再分别用两点距离公式即可,(3)将a=2-2b代入s的表达式,得到b的一个二次函数.
b,再分别用两点距离公式即可,(3)将a=2-2b代入s的表达式,得到b的一个二次函数.当b=0.8时,s最小.
本试题主要是考查了建立直角坐标系来表示面积,得到二次函数的最值的问题。
根据已知条件先以边CA、CB所在直线分别为x轴、y轴建立直角坐标系,,设A(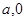 )、B(0,b),P点的坐标为(x,y),由条件可知
)、B(0,b),P点的坐标为(x,y),由条件可知 =
=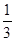
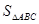 ,可求出x=
,可求出x=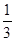
 ,y=
,y=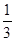 b,再运用两点距离公式得到关于b的表达式,进而得到面积的最小值。
b,再运用两点距离公式得到关于b的表达式,进而得到面积的最小值。
根据已知条件先以边CA、CB所在直线分别为x轴、y轴建立直角坐标系,,设A(
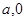 )、B(0,b),P点的坐标为(x,y),由条件可知
)、B(0,b),P点的坐标为(x,y),由条件可知 =
=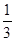
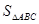 ,可求出x=
,可求出x=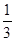
 ,y=
,y=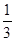 b,再运用两点距离公式得到关于b的表达式,进而得到面积的最小值。
b,再运用两点距离公式得到关于b的表达式,进而得到面积的最小值。
练习册系列答案
 高效智能课时作业系列答案
高效智能课时作业系列答案 捷径训练检测卷系列答案
捷径训练检测卷系列答案
相关题目
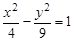 有相同的渐近线,且一条准线为
有相同的渐近线,且一条准线为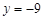 ,求双曲线C的方程;
,求双曲线C的方程; (Ⅱ)已知圆截
(Ⅱ)已知圆截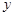 轴所得弦长为6,圆心在直线
轴所得弦长为6,圆心在直线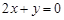 上,并与
上,并与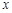 轴相切,求该圆的方程.
轴相切,求该圆的方程. 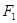 、
、 ,以
,以 为边作正三角形,若双曲线恰好平分另外两边,则双曲线的离心率为( )
为边作正三角形,若双曲线恰好平分另外两边,则双曲线的离心率为( )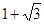
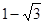

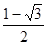
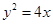 上一点
上一点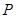 引其准线的垂线,垂足为
引其准线的垂线,垂足为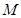 ,设抛物线的焦点为
,设抛物线的焦点为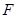 ,且
,且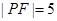 ,则
,则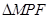 的面积为 .
的面积为 .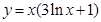 在点(1,1)处的切线方程为______
在点(1,1)处的切线方程为______ 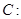
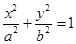
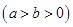 的左右焦点分别是
的左右焦点分别是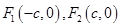 ,直线
,直线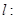
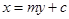 与椭圆
与椭圆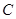 交于两点
交于两点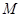 ,
,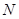 .当
.当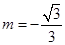 时,M恰为椭圆
时,M恰为椭圆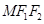 的周长为6.
的周长为6.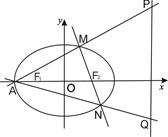
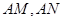 与直线
与直线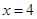 分别相交于点
分别相交于点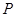 ,
,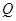 ,问当
,问当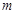
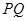 为直径的圆被
为直径的圆被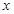 轴截得的弦长是否为定值?若是,求出这个定值,
轴截得的弦长是否为定值?若是,求出这个定值,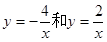 的图象交于点A和点B,若点C是x轴上任意一点,连接AC、BC,
的图象交于点A和点B,若点C是x轴上任意一点,连接AC、BC,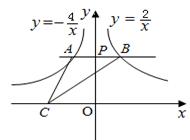
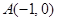 ,
,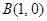 ,动点
,动点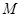 的轨迹曲线
的轨迹曲线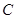 满足
满足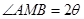 ,
,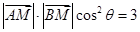 ,过点
,过点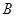 的直线交曲线
的直线交曲线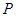 、
、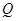 两点.
两点.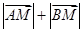 的值,并写出曲线
的值,并写出曲线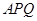 面积的最大值.
面积的最大值.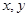 为正实数,
为正实数,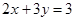 ,则
,则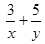 的最小值为 .
的最小值为 .