Question

已知函数．

   （Ⅰ）若在上是减函数，求的取值范围；

   （Ⅱ）函数是否既有极大值又有极小值？若存在，求的取值范围；若不存在，请说明理由．

Answer 1

解：（Ⅰ）=                          

     ∵在上为减函数，∴时恒成立． 

即恒成立．设，则=．

∵时＞4，∴，∴在上递减，      

∴g() ＞g()=3，∴≤3．                                  

（Ⅱ）若既有极大值又有极小值，则首先必须=0有两个不同正根，

即 有两个不同正根。                     

令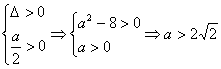

∴当＞2时，=0有两个不等的正根              

不妨设，由=－（）=－知：

时＜0，时＞0，时＜0，

∴当a＞2时既有极大值又有极小值．