题目内容
已知函数y=asinx+bcosx+c的图象上有一个最低点(| 11π |
| 6 |
(Ⅰ)如果x=0时,y=-
| ||
| 2 |
(Ⅱ)如果将图象上每个点的纵坐标不变,横坐标缩小到原来的
| 3 |
| π |
分析:(Ⅰ)利用辅助角公式对函数解析式化简整理,把最低点坐标代入求得φ和a,b和c的关系,表示出函数的解析式,把x=0代入即可求得a,b和c.
(Ⅱ)依据题意可求得变换后函数的解析式,进而可知方程f(x)=3的正根就是直线y=3与y=f(x)的图象交点的横坐标,通过它们成等差数列,判断出直线y=3满足以上要求只能有三个位置:一是过图象最高点且和x轴平行的直线l1,二是过图象最低点且和x轴平行的直线l2,三是和l1、l2平行且等距的直线l3,根据最低点排除l2.假若直线y=3在l1,交点间隔为一个周期6,即正根的公差为6,不合题意,所以y=3只能在l3位置,求得c,则函数的解析式求得正根检验后符合题意,函数的解析式可得.
(Ⅱ)依据题意可求得变换后函数的解析式,进而可知方程f(x)=3的正根就是直线y=3与y=f(x)的图象交点的横坐标,通过它们成等差数列,判断出直线y=3满足以上要求只能有三个位置:一是过图象最高点且和x轴平行的直线l1,二是过图象最低点且和x轴平行的直线l2,三是和l1、l2平行且等距的直线l3,根据最低点排除l2.假若直线y=3在l1,交点间隔为一个周期6,即正根的公差为6,不合题意,所以y=3只能在l3位置,求得c,则函数的解析式求得正根检验后符合题意,函数的解析式可得.
解答:解:(Ⅰ)原函数可化为y=
sin(x+φ)+c
(其中φ为辅助角,满足cosφ=
,且sinφ=
),
因为(
,-1)是它的最低点,
所以
,
解得φ=2kπ-
(k∈Z)且
=c+1.
所以y=(c+1)sin(x-
)+c.
又x=0时,y=-
,所以c=0,b=-
,a=
;
(Ⅱ)因为y=(c+1)sin(x-
)+c,
按题给变换后得f(x)=(c+1)sin
x+c
方程f(x)=3的正根就是直线y=3与y=f(x)的图象交点的横坐标,
它们成等差数列,即y=3与y=f(x)相邻交点间的距离都相等.
直线y=3满足以上要求只能有三个位置:
一是过图象最高点且和x轴平行的直线l1,
二是过图象最低点且和x轴平行的直线l2,
三是和l1、l2平行且等距的直线l3,而图象最低点为(
,-1),
故不可能是l2.假若直线y=3在l1,交点间隔为一个周期6,
即正根的公差为6,不合题意,所以y=3只能在l3位置,
所以c=3,f(x)=4sin
x+3,此时由sin
x=0得x=3k,
正根可组成一个公差为3的等差数列,符合题意.
∴f(x)=4sin
x+3.
| a2+b2 |
(其中φ为辅助角,满足cosφ=
| a | ||
|
| b | ||
|
因为(
| 11π |
| 6 |
所以
|
解得φ=2kπ-
| 7π |
| 3 |
| a2+b2 |
所以y=(c+1)sin(x-
| π |
| 3 |
又x=0时,y=-
| ||
| 2 |
| ||
| 2 |
| 1 |
| 2 |
(Ⅱ)因为y=(c+1)sin(x-
| π |
| 3 |
按题给变换后得f(x)=(c+1)sin
| π |
| 3 |
方程f(x)=3的正根就是直线y=3与y=f(x)的图象交点的横坐标,
它们成等差数列,即y=3与y=f(x)相邻交点间的距离都相等.
直线y=3满足以上要求只能有三个位置:
一是过图象最高点且和x轴平行的直线l1,
二是过图象最低点且和x轴平行的直线l2,
三是和l1、l2平行且等距的直线l3,而图象最低点为(
| 11π |
| 6 |
故不可能是l2.假若直线y=3在l1,交点间隔为一个周期6,
即正根的公差为6,不合题意,所以y=3只能在l3位置,
所以c=3,f(x)=4sin
| π |
| 3 |
| π |
| 3 |
正根可组成一个公差为3的等差数列,符合题意.
∴f(x)=4sin
| π |
| 3 |
点评:本题主要考查了三角函数的化简求值,等差数列的应用,三角函数的图象变换.考查了学生分析问题的能力和推理能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知函数y=Asin(ωx+φ),在同一周期内,当x=
时,取最大值y=2,当x=
时,取得最小值y=-2,那么函数的解析式为( )
| π |
| 12 |
| 7π |
| 12 |
A、y=
| ||||
B、y=2sin(2x+
| ||||
C、y=2sin(
| ||||
D、y=2sin(2x+
|
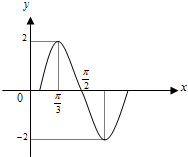 已知函数y=Asin(ωx+∅)(A>0,ω>0,-π≤∅≤π)一个周期的图象(如图),则这个函数的一个解析式为( )
已知函数y=Asin(ωx+∅)(A>0,ω>0,-π≤∅≤π)一个周期的图象(如图),则这个函数的一个解析式为( )A、y=2sin(
| ||||
B、y=2sin(3x+
| ||||
C、y=2sin(3x-
| ||||
D、y=2sin(3x-
|
 已知函数
已知函数 已知函数
已知函数