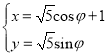题目内容
【题目】某产品自生产并投入市场以来，生产企业为确保产品质量，决定邀请第三方检测机构对产品进行质量检测，并依据质量指标Z来衡量产品的质量.当
时，产品为优等品；当
时，产品为一等品；当
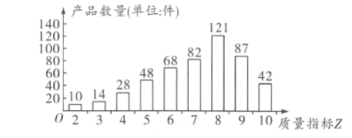
时，产品为二等品.第三方检测机构在该产品中随机抽取500件，绘制了这500件产品的质量指标
的条形图.用随机抽取的500件产品作为样本，估计该企业生产该产品的质量情况，并用频率估计概率．
（1）从该企业生产的所有产品中随机抽取4件，求至少有1件优等品的概率；
（2）现某人决定购买80件该产品.已知每件成本1000元，购买前，邀请第三方检测机构对要购买的80件产品进行抽样检测，买家、企业及第三方检测机构就检测方案达成以下协议：从80件产品中随机抽出4件产品进行检测，若检测出3件或4件为优等品，则按每件1600元购买，否则按每件1500元购买，每件产品的检测费用250元由企业承担．记企业的收益为X元，求X的分布列与数学期望.
【答案】(1)
;(2)分布列见解析，数学期望为41500.
【解析】
（1）先求出从样本中随机取一件为优等品的概率，再求从该企业生产的所有产品中随机抽取4件，没有一件是优等品的概率，从而可求出至少有一件是优等品的概率.
（2）由题意求出检测出3件或4件为优等品时及检测出的优等品低于3件时的
的值，结合第一问求出
，
，从而可得的分布列，即可计算其数学期望.
（1）解：由题意知，500件产品中共有优等品
件，
则从样本中随机取一件为优等品的概率为
，
所以从该企业生产的所有产品中随机抽取4件，没有一件是优等品的概率为
，
则随机抽取4件，至少有1件优等品的概率为
.
（2）解：检测出3件或4件为优等品时
，
检测出的优等品低于3件时，
，由题意知
，
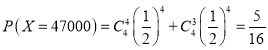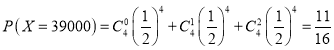，故X的分布列为
| 47000 | 39000 |
|
|
|
所以数学期望
.
