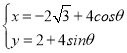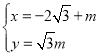题目内容
【题目】在直角坐标系xOy中,曲线C1的参数方程为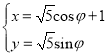 (φ为参数),以坐标原点O为极点,x轴的正半轴为极轴,建立极坐标系.
(φ为参数),以坐标原点O为极点,x轴的正半轴为极轴,建立极坐标系.
(1)求C1的极坐标方程;
(2)若C1与曲线C2:ρ=2sinθ交于A,B两点,求|OA||OB|的值.
【答案】(1)ρ2﹣2ρcosθ﹣4=0;(2)![]() .
.
【解析】
(1)直接利用转换关系,把参数方程极坐标方程和直角坐标方程之间进行转换.
(2)利用两曲线间的位置关系的应用求出交点的坐标,进一步利用两点间的距离公式的应用求出结果.
(1)曲线C1的参数方程为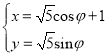 (φ为参数),
(φ为参数),
所以C1的普通方程为![]() ,即
,即![]() ,
,
化为极坐标方程为ρ2﹣2ρcosθ﹣4=0.
(2)由于若C1与曲线C2:ρ=2sinθ交于A,B两点,
曲线C2:ρ=2sinθ转换为直角坐标方程为x2+y2=2y,
所以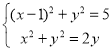 ,解得
,解得![]() 或
或![]()
故![]() ,所以
,所以![]() .
.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
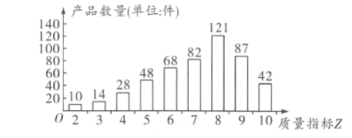
【题目】党的十九大明确把精准脱贫作为决胜全面建成小康社会必须打好的三大攻坚战之一,为坚决打赢脱贫攻坚战,某帮扶单位考察了甲乙两种不同的农产品加工生产方式,现对两种生产方式加工的产品质量进行测试并打分对比,得到如下数据:
生产方式甲 | 分值区间 |
|
|
|
|
|
频数 | 20 | 30 | 100 | 40 | 10 | |
生产方式乙 | 分值区间 |
|
|
|
|
|
频数 | 25 | 35 | 60 | 50 | 30 |
其中产品质量按测试指标可划分为:指标在区间![]() 上的为特优品,指标在区间
上的为特优品,指标在区间![]() 上的为一等品,指标在区间
上的为一等品,指标在区间![]() 上的为二等品.
上的为二等品.
(1)用事件![]() 表示“按照生产方式甲生产的产品为特优品”,估计
表示“按照生产方式甲生产的产品为特优品”,估计![]() 的概率;
的概率;
(2)填写下面列联表,并根据列联表判断能否有![]() 的把握认为“特优品”与生产方式有关?
的把握认为“特优品”与生产方式有关?
特优品 | 非特优品 | |
生产方式甲 | ||
生产方式乙 |
(3)根据打分结果对甲乙两种生产方式进行优劣比较.
附表:
| 0.10 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
参考公式: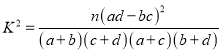 ,其中
,其中![]() .
.