Question

【题目】已知椭圆的长轴长为，右顶点到左焦点的距离为，、分别为椭圆的左、右两个焦点.

（1）求椭圆的方程；

（2）已知椭圆的切线（与椭圆有唯一交点）的方程为，切线与直线和直线分别交于点、，求证：为定值，并求此定值；

（3）设矩形的四条边所在直线都和椭圆相切（即每条边所在直线与椭圆有唯一交点），求矩形的面积的取值范围.

Answer 1

【答案】（1）；（2）证明见解析，；（3）

【解析】

（1）由长轴长可得,由右顶点到左焦点的距离为,进而求解即可；

（2）联立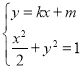可得,由相切可得,则,分别求得,,将代入,进而求解即可；

（3）分别讨论与的情况,当时,设直线为,则,联立直线与椭圆方程,令可得,即可代回求得直线的方程,进而求得直线与直线的距离,同理求得直线与直线的距离,从而利用均值不等式求解.

（1）由题,因为,,

所以,,则,

所以椭圆的标准方程为.

（2）证明:由（1）,

联立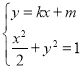可得,

所以,即,

对于切线:,

当时,；当时,,

所以,

,

所以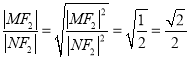,为定值.

（3）由题,当时,；

当时,设边所在直线为切线:,

所以,

联立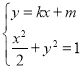可得,

则,即,

所以直线的方程为；直线的方程为,

所以直线和直线的距离为,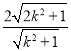

同理,直线和直线的距离为,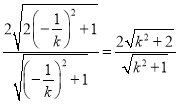

所以,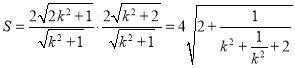

因为,当且仅当,即时等号成立,

所以,

综上,