题目内容
已知极坐标系的极点在直角坐标系的原点处,极轴与 轴的正半轴重合.
轴的正半轴重合.
直线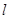 的参数方程为:
的参数方程为: (t为参数),曲线
(t为参数),曲线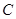 的极坐标方程为:
的极坐标方程为: .
.
(Ⅰ)写出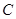 的直角坐标方程,并指出
的直角坐标方程,并指出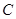 是什么曲线;
是什么曲线;
(Ⅱ)设直线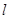 与曲线
与曲线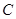 相交于
相交于 、
、 两点,求
两点,求 值.
值.
(Ⅰ)曲线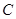 的直角坐标方程为
的直角坐标方程为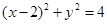 ,它是以
,它是以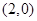 为圆心,
为圆心,
半径为 的圆.
的圆.
(Ⅱ)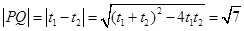 。
。
解析试题分析:(Ⅰ)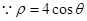 ,
,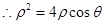 ,………………………………………………………………2分
,………………………………………………………………2分
由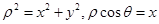 得:
得: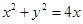
所以曲线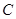 的直角坐标方程为
的直角坐标方程为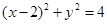 ,…………………………4分
,…………………………4分
它是以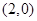 为圆心,半径为
为圆心,半径为 的圆. …………………………………………5分
的圆. …………………………………………5分
(Ⅱ)把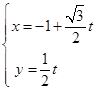 代入
代入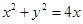 整理得
整理得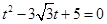 ,……7分
,……7分
设其两根分别为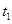 、
、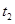 ,则
,则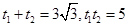 ,…………………………8分
,…………………………8分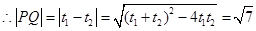 ……………………………………10分
……………………………………10分
另解:
化直线参数方程为普通方程,然后求圆心到直线距离,再用垂径定理求得 的值.
的值.
考点:本题主要考查极坐标方程与普通方程的互化,参数方程的应用。
点评:中档题,学习参数方程、极坐标,其中一项基本的要求是几种不同形式方程的互化,其次是应用极坐标、参数方程,简化解题过程。参数方程的应用,往往可以把曲线问题转化成三角问题,也可在计算弦长时发挥较好作用。

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
200辆汽车通过某一段公路时的时速的频率分布直方图如右图所示,则时速在[60,70)的汽车大约( )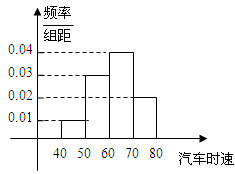
| A.30辆 | B.40辆 | C.60辆 | D.80辆 |
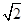 倍.
倍.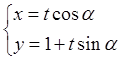 (t为参数,0 ≤ α < π).以原点为极点,x轴的正半轴为极轴建立极坐标系.已知曲线C的极坐标方程为ρcos2θ = 4sinθ.
(t为参数,0 ≤ α < π).以原点为极点,x轴的正半轴为极轴建立极坐标系.已知曲线C的极坐标方程为ρcos2θ = 4sinθ.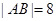 ,求α的值.
,求α的值.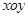 中,直线
中,直线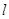 的方程为
的方程为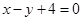 ,曲线
,曲线 的参数方程为
的参数方程为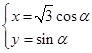 (
(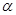 为参数)
为参数)  为极点,以
为极点,以 轴正半轴为极轴)中,点
轴正半轴为极轴)中,点 的极坐标为(4,
的极坐标为(4,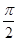 ),判断点
),判断点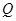 是曲线
是曲线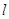 经过点
经过点 ,倾斜角
,倾斜角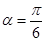 ,
,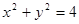 相交于
相交于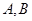 两点,求点
两点,求点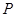 到
到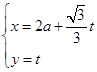 (
(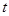 为参数,
为参数,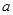 为常数且
为常数且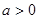 )被以原点为极点,
)被以原点为极点, 轴的正半轴为极轴,方程为
轴的正半轴为极轴,方程为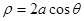 的曲线所截,求截得的弦长.
的曲线所截,求截得的弦长.
 (
( 为参数)和直线
为参数)和直线 (其中为参数,
(其中为参数, 为直线的倾斜角),如果直线与圆
为直线的倾斜角),如果直线与圆 有公共点,求
有公共点,求 人,现用分层抽样的方法从该
人,现用分层抽样的方法从该


