题目内容
在直接坐标系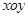 中,直线
中,直线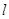 的方程为
的方程为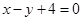 ,曲线
,曲线 的参数方程为
的参数方程为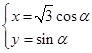 (
(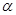 为参数)
为参数)
(I)已知在极坐标(与直角坐标系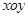 取相同的长度单位,且以原点
取相同的长度单位,且以原点 为极点,以
为极点,以 轴正半轴为极轴)中,点
轴正半轴为极轴)中,点 的极坐标为(4,
的极坐标为(4,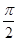 ),判断点
),判断点 与直线
与直线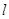 的位置关系;
的位置关系;
(II)设点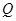 是曲线
是曲线 上的一个动点,求它到直线
上的一个动点,求它到直线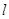 的距离的最小值.
的距离的最小值.
(Ⅰ)点 在直线
在直线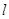 上(Ⅱ)
上(Ⅱ)
解析试题分析:(I)把极坐标系下的点 化为直角坐标,得
化为直角坐标,得 .
.
因为点 的直角坐标(0,4)满足直线
的直角坐标(0,4)满足直线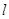 的方程
的方程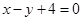 ,
,
所以点 在直线
在直线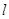 上. ……5分
上. ……5分
(II)设点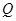 的坐标为
的坐标为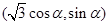 ,则点
,则点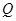 到直线
到直线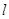 的距离为
的距离为  .
.
由此得,当 时,
时, 取得最小值,且最小值为
取得最小值,且最小值为 . ……10分
. ……10分
考点:本小题主要考查极坐标和直角坐标的互化和参数方程的应用,以及三角函数的化简求值.
点评:解决此类问题的关键是正确进行极坐标和直角坐标的转化,利用公式求解即可,另外,参数方程在求最值时比较好用,要灵活应用.

练习册系列答案
相关题目
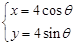 (
(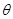 为参数),直线l经过点P(2,2),倾斜角
为参数),直线l经过点P(2,2),倾斜角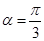 。(1)写出圆的标准方程和直线l的参数方程;
。(1)写出圆的标准方程和直线l的参数方程;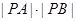 的值。
的值。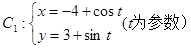 (t为参数),
(t为参数),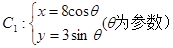
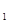 ,C
,C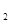 的方程为普通方程,并说明它们分别表示什么曲线;
的方程为普通方程,并说明它们分别表示什么曲线;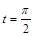 ,Q为C
,Q为C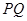 中点
中点 到直线
到直线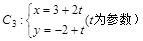 (t为参数)距离的最小值。
(t为参数)距离的最小值。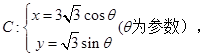 直线
直线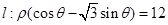
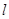 的极坐标方程和曲线的参数方程分别化为直角坐标方程和普通方程;
的极坐标方程和曲线的参数方程分别化为直角坐标方程和普通方程; 轴的正半轴重合.
轴的正半轴重合.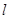 的参数方程为:
的参数方程为: (t为参数),曲线
(t为参数),曲线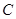 的极坐标方程为:
的极坐标方程为: .
. 、
、 两点,求
两点,求 值.
值.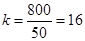 ,即每16人抽取一个人.在1~16中随机抽取一个数,如果抽到的是7,则从33~48这16个数中应取的数是( )
,即每16人抽取一个人.在1~16中随机抽取一个数,如果抽到的是7,则从33~48这16个数中应取的数是( )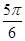 .
.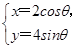 (θ为参数)交于A,B两点,求|PA|·|PB|.
(θ为参数)交于A,B两点,求|PA|·|PB|. 中,曲线
中,曲线 的参数方程为
的参数方程为 ,
, 为极点,
为极点, 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线 的极坐标方程为
的极坐标方程为 .
. 时,曲线
时,曲线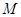 、
、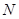 两点,求以线段
两点,求以线段 为直径的圆的直角坐标方程.
为直径的圆的直角坐标方程.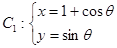
 为参数
为参数 ,在曲线
,在曲线 上求一点
上求一点 ,使它到直线
,使它到直线
 为参数
为参数