题目内容
(本小题12分)已知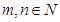 ,且点A
,且点A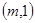 和点B
和点B 都在椭圆
都在椭圆 内部,
内部,
(1)请列出有序数组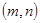 的所有可能结果;
的所有可能结果;
(2)记“使得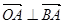 成立的
成立的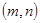 ”为事件A,求事件A发生的概率。
”为事件A,求事件A发生的概率。
(1)(0,0),(0,1),(0,2),(1,0),(1,1),(1,2),(2,0),(2,1),(2,2),(3,0),(3,1),(3,2)共12个基本事件。
(2)事件A发生的概率为 。
。
解析试题分析:(1)先利用椭圆的几何性质得到参数n,m的满足的自然数的值,然后利用点的坐标的表示,确定出所有的有序数组。
(2)将向量的垂直问题,运用参数m表示得到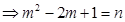 ,即为
,即为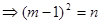 ,进而从所有结果中找到事件发生的基本事件数即可。
,进而从所有结果中找到事件发生的基本事件数即可。
解:∵点A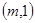 在椭圆内且
在椭圆内且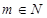 ,
,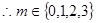
又点B 在椭圆内且
在椭圆内且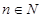 ,
,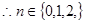
∴有序数组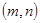 的所有可能结果为:
的所有可能结果为:
(0,0),(0,1),(0,2),(1,0),(1,1),(1,2),(2,0),(2,1),(2,2),(3,0),(3,1),(3,2)共12个基本事件。
由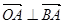
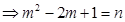 即
即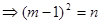
故事件A包含的基本事件为(0,1)、(1,0)、(2,1)共3个。∴P(A)=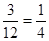
答:事件A发生的概率为
考点:本试题主要考查了古典概型概率的求解运用。
点评:解决该试题的关键是弄清楚点在椭圆内时,参数m,n的满足的值,然后列举法得到试验的全部结果,结合古典概型求解得到。

练习册系列答案
相关题目
 的离心率为
的离心率为 ,焦点在
,焦点在 轴上,且长轴长为10,曲线
轴上,且长轴长为10,曲线 上的点与椭圆
上的点与椭圆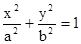 (a>b>0)的一个顶点为A(2,0),离心率为
(a>b>0)的一个顶点为A(2,0),离心率为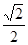 ,直线y=k(x-1)与椭圆C交于不同的两点M、N.
,直线y=k(x-1)与椭圆C交于不同的两点M、N.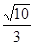 时,求k的值.
时,求k的值. 的左,右焦点分别为
的左,右焦点分别为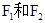 ,过
,过 的直线L与椭圆C相交 A,B于两点,且直线L的倾斜角为
的直线L与椭圆C相交 A,B于两点,且直线L的倾斜角为 ,点
,点 到直线L的距离为
到直线L的距离为 ,
, 求椭圆C的方程.(12分)
求椭圆C的方程.(12分) 的离心率
的离心率 ,过右焦点
,过右焦点 的直线
的直线 与椭圆
与椭圆 相交于
相交于 两点,当直线
两点,当直线 到直线
到直线 .
. ,使得当直线
,使得当直线 成立?若存在,求出所有满足条件的点
成立?若存在,求出所有满足条件的点 ,左右焦点分别为
,左右焦点分别为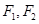 ,
, 上一点
上一点 满足
满足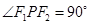 ,求
,求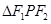 的面积;
的面积; 交
交 ,线段
,线段 的中点为
的中点为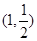 ,求直线
,求直线 :
: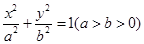 的两个焦点为
的两个焦点为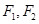 ,点
,点 在椭圆
在椭圆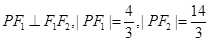 .
.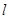 过圆
过圆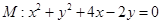 的圆心,交椭圆
的圆心,交椭圆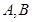 两点,且
两点,且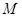 对称,求直线
对称,求直线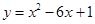 与坐标轴的交点都在圆上.
与坐标轴的交点都在圆上. 交于A,B两点,且
交于A,B两点,且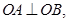 求a的值.
求a的值.