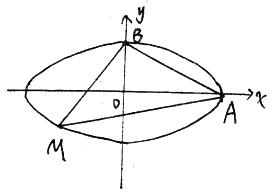
题目内容
(本小题12分)椭圆 :
: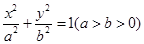 的两个焦点为
的两个焦点为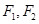 ,点
,点 在椭圆
在椭圆 上,且
上,且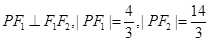 .
.
(Ⅰ)求椭圆 的方程;
的方程;
(Ⅱ)若直线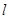 过圆
过圆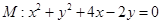 的圆心,交椭圆
的圆心,交椭圆 于
于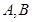 两点,且
两点,且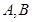 关于点
关于点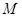 对称,求直线
对称,求直线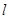 的方程。
的方程。
(1)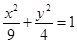 (2)
(2)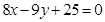
解析试题分析:
(Ⅰ)依题可设椭圆方程为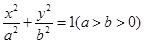 ,
,
因为点 在椭圆
在椭圆 上,所以
上,所以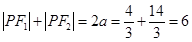 ,则
,则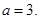 ……2分
……2分
在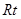 △
△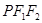 中,
中,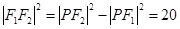 , 故
, 故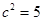 ,
,
从而 ,
,
所以椭圆 的方程为
的方程为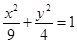 . ……4分
. ……4分
(Ⅱ)(解法一)设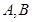 的坐标分别为
的坐标分别为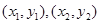 。
。
已知圆的方程为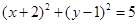 ,所以圆心
,所以圆心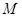 的坐标为
的坐标为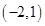 .
.
从而可设直线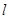 的方程为
的方程为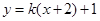 ,
,
代入椭圆 的方程得
的方程得 .……8分
.……8分
因为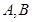 关于点
关于点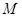 对称. 所以
对称. 所以 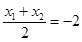 且
且
解得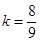 ,所以直线
,所以直线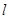 的方程为 即
的方程为 即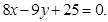
(经检验,所求直线方程符合题意) ……12分
(解法二)已知圆的方程为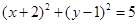 ,故圆心
,故圆心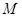 为
为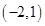 .
.
设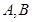 的坐标分别为
的坐标分别为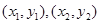 。
。
由题意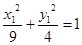 ①
①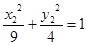 ②
②
由①-②得: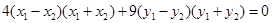 ③
③
因为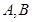 关于点
关于点 对称,所以
对称,所以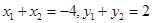 ,
,
代入③得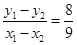 , 即直线
, 即直线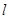 的斜率
的斜率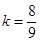 , ……10分
, ……10分
所以直线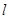 的方程为
的方程为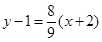 ,即
,即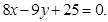
(经检验,所求直线方程符合题意.) ……12分
考点:本小题主要考查直线与椭圆的位置关系,考查学生分析问题、解决问题的能力和计算能力.
点评:直线与圆锥曲线(椭圆、双曲线、抛物线等)的位置关系是每年高考的重点也是难点,学生在复习备考时,要了解直线与圆锥曲线的位置关系问题的解决方法,尤其是通性通法和常用技巧,如设而不求、点差法等,另外还要注意计算能力的培养与训练,养成良好的运算习惯.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
 交于A,B两点.
交于A,B两点.  与抛物线
与抛物线 交于不同两点A、B,F为抛物线的焦点。
交于不同两点A、B,F为抛物线的焦点。 的重心G的轨迹方程;
的重心G的轨迹方程; 的外接圆的方程。
的外接圆的方程。 ,且点A
,且点A 和点B
和点B 都在椭圆
都在椭圆 内部,
内部,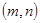 的所有可能结果;
的所有可能结果;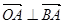 成立的
成立的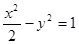 的左、右顶点分别为A1、A2,垂直于x轴的直线m与双曲线C交于不同的两点
的左、右顶点分别为A1、A2,垂直于x轴的直线m与双曲线C交于不同的两点 。
。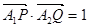 ,求点T的坐标;
,求点T的坐标;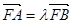 ,若
,若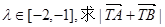 (T为(1)中的点)的取值范围。
(T为(1)中的点)的取值范围。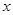 O
O 中,直线
中,直线 与抛物线
与抛物线 =2
=2 =3”是真命题;
=3”是真命题;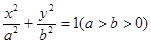 的右焦点为
的右焦点为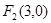 ,离心率为
,离心率为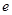 .
.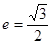 ,求椭圆的方程; (2)设直线
,求椭圆的方程; (2)设直线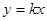 与椭圆相交于
与椭圆相交于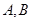 两点,
两点,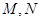 分别为线段
分别为线段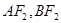 的中点.若坐标原点
的中点.若坐标原点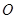 在以
在以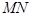 为直径的圆上,且
为直径的圆上,且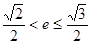 ,求
,求 的取值范围.
的取值范围. 、B
、B 、C
、C 三点,过坐标原点O的直线
三点,过坐标原点O的直线 与抛物线交于M、N两点.分别过点C、D
与抛物线交于M、N两点.分别过点C、D 作平行于
作平行于 轴的直线
轴的直线 、
、 .(1)求抛物线对应的二次函数的解析式;
.(1)求抛物线对应的二次函数的解析式; 表示),并证明M、N两
表示),并证明M、N两
 轴,短轴所在直线为
轴,短轴所在直线为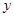 轴,建立平面直角坐标系,如图所示:
轴,建立平面直角坐标系,如图所示: