题目内容
7.某省为了研究雾霾天气的治理,一课题组对省内24个城市进行了空气质量的调查,按地域特点把这些城市分成了甲、乙、丙三组.已知三组城市的个数分别为4,8,12,课题组用分层抽样的方法从中抽取6个城市进行空气质量的调查.(I)求每组中抽取的城市的个数;
(II)从已抽取的6个城市中任抽两个城市,求两个城市不来自同一组的概率.
分析 (Ⅰ)根据分层抽样方法的特点,求出从甲、乙、丙组中应抽取的城市数;
(Ⅱ)利用列举法求出基本事件数,计算对应的概率即可.
解答 解:(Ⅰ)设从甲、乙、丙三组城市中应抽取的个数分别为x、y、z,
则由题意得$\frac{x}{4}$=$\frac{y}{8}$=$\frac{z}{12}$=$\frac{6}{24}$,…(3分)
解得,x=1、y=2、z=3;…(4分)
故从甲、乙、丙组中应抽取的城市的个数分别为:1,2,3;…(5分)
(Ⅱ)由(Ⅰ)可知,从甲、乙、丙组中应抽取的城市的个数分别为为:1,2,3,
记甲组中已抽取的城市为a1,乙组中已抽取的城市为b1、b2,
丙组中已抽取的城市为c1、c2、c3;…(6分)
从已抽取的6个城市中任抽两个城市的所有可能为:
a1b1、a1b2、a1c1、a1c2、a1c3、b1b2、b1c1、b1c2、b1c3、
b2c1、b2c2、b2c3、c1c2、c1c3、c2c3共15种;…(8分)
设“抽取的两个城市不来自同一组”为事件A,
则事件A包括a1b1、a1b2、a1c1、a1c2、a1c3、b1c1、b1c2、b1c3、
b2c1、b2c2、b2c3共11种;…(10分)
所以P(A)=$\frac{11}{15}$;
即从已抽取的6个城市中任抽两个城市,两个城市不来自同一组的概率为$\frac{11}{15}$.…(12分)
点评 本题考查了分层抽样方法的应用问题,也考查了用列举法求古典概型的概率问题,是基础题目.

练习册系列答案
 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案
相关题目
15.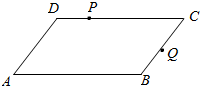 如图在平行四边形ABCD中,已知AB=3,AD=2,∠DAB=60°,2$\overrightarrow{DP}$=$\overrightarrow{PC}$,$\overrightarrow{BQ}$=$\overrightarrow{QC}$,则$\overrightarrow{AP}$•$\overrightarrow{AQ}$=( )
如图在平行四边形ABCD中,已知AB=3,AD=2,∠DAB=60°,2$\overrightarrow{DP}$=$\overrightarrow{PC}$,$\overrightarrow{BQ}$=$\overrightarrow{QC}$,则$\overrightarrow{AP}$•$\overrightarrow{AQ}$=( )
 如图在平行四边形ABCD中,已知AB=3,AD=2,∠DAB=60°,2$\overrightarrow{DP}$=$\overrightarrow{PC}$,$\overrightarrow{BQ}$=$\overrightarrow{QC}$,则$\overrightarrow{AP}$•$\overrightarrow{AQ}$=( )
如图在平行四边形ABCD中,已知AB=3,AD=2,∠DAB=60°,2$\overrightarrow{DP}$=$\overrightarrow{PC}$,$\overrightarrow{BQ}$=$\overrightarrow{QC}$,则$\overrightarrow{AP}$•$\overrightarrow{AQ}$=( )| A. | $\frac{13}{2}$ | B. | $\frac{15}{2}$ | C. | $\frac{17}{2}$ | D. | $\frac{19}{2}$ |
2.若点P(x,y)在函数y=$\frac{1}{{x}^{2}}$+$\sqrt{-x}$的图象上,则点P在平面直角坐标系中的( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
17.设函数f(x)是定义在(-∞,0)上的可导函数,其导函数为f′(x),且有2f(x)+xf′(x)>x2,则不等式(x+2015)2f(x+2015)-4f(-2)>0的解集为( )
| A. | (-2016,0) | B. | (-2012,0) | C. | (-∞,-2016) | D. | (-∞,-2017) |