题目内容
已知集合A={x|
≤0},B={x|y=ln(-x2+12x-20)},C={x|5-a<x<a}
(1)求A∪B,(∁RA)∩B;
(2)若C⊆(A∪B),求a的取值范围.
| x-3 |
| x-7 |
(1)求A∪B,(∁RA)∩B;
(2)若C⊆(A∪B),求a的取值范围.
解(1)A={x|
≤0}={x|3≤x<7},B={x|2<x<10},
∴A∪B={x|2<x<10},
∵CRA={x|x<3或x≥7},
∴(CRA)∩B={x|2<x<3或7≤x<10};
(2)由(1)知A∪B={x|2<x<10},
①当C=φ时,满足C⊆(A∪B),此时5-a≥a,得a≤
;
②当C≠φ时,要C⊆(A∪B),
则
,解得
<a≤3.
由①②得可知a的取值范围:a≤3.
| x-3 |
| x-7 |
∴A∪B={x|2<x<10},
∵CRA={x|x<3或x≥7},
∴(CRA)∩B={x|2<x<3或7≤x<10};
(2)由(1)知A∪B={x|2<x<10},
①当C=φ时,满足C⊆(A∪B),此时5-a≥a,得a≤
| 5 |
| 2 |
②当C≠φ时,要C⊆(A∪B),
则
|
| 5 |
| 2 |
由①②得可知a的取值范围:a≤3.

练习册系列答案
相关题目
 ,则集合A∩B的元素个数为( )
,则集合A∩B的元素个数为( )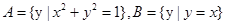 ,则
,则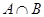 =
=

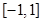

 ( )
( )



 ,
, ,
, ,则
,则 等于 ( )
等于 ( )