题目内容
设集合A={x|x2+3x-4=0}，B={x|ax+2=0，x∈R}，若A∩B=B，求实数a的取值范围．
集合A={x|x2+3x-4=0}={1，-4}，
∵A∩B=B，
∴B⊆A，
若a=0，则B=∅，满足条件B⊆A，
若a≠0，则B={x|ax+2=0，x∈R}={x|x=
}，
要使B⊆A成立，
则-
=1或-
=-4，
解得a=-2或a=
，
综上：a=-2或a=
，或a=0．
∵A∩B=B，
∴B⊆A，
若a=0，则B=∅，满足条件B⊆A，
若a≠0，则B={x|ax+2=0，x∈R}={x|x=
| -2 |
| a |
要使B⊆A成立，
则-
| 2 |
| a |
| 2 |
| a |
解得a=-2或a=
| 1 |
| 2 |
综上：a=-2或a=
| 1 |
| 2 |
练习册系列答案
周周清检测系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
.
;
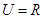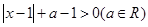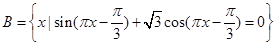，若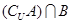
恰有3个元素，求
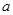的取值范围.
，
，则
（ ）
