Question

 给出下列命题：

①a,b都为正数时,不等式a+b≥2才成立。

②y=x+的最小值为2。

③y=sinx+()的最小值为2.

④当x>0时，y=x²+16x≥2,当x²＝16x时，即x=16,y取最小值512。

其中错误的命题是           。

 

Answer 1

【答案】

①②③④。

【解析】

试题分析：①a+b≥2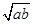成立的充要条件是；

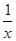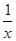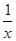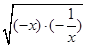②当x>0,y=x+≥2;当x<0时,y=x+=-(-x-)≤-2=-2;

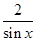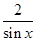③y=sinx+≥2，等号成立的条件是sinx＝，即sinx＝，

而当时，0<sinx≤1，故等号不成立，y的最小值可通过单调性的定义判断y=t+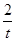(t=sinx)在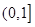上单调递减，从而y_min=1+=3;

④“2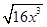”不是定值，因此该命题也不对。y=x²+16x在x单调递增，无最小值。

考点：本题主要考查函数的有界性、单调性、不等式均值定理的应用。

点评：应用均值定理，应注意“一正、二定、三相等”。常见错误是忽视等号成立的条件。