题目内容
已知集合A={f(x)|f2(x)-f2(y)=f(x+y)•f(x-y),x、y∈R},有下列命题:
①若f(x)=
,则f(x)∈A;
②若f(x)=kx,则f(x)∈A;
③若f(x)∈A,则y=f(x)可为奇函数;
④若f(x)∈A,则对任意不等实数x1,x2,总有
<0成立.
其中所有正确命题的序号是______.(填上所有正确命题的序号)
①若f(x)=
|
②若f(x)=kx,则f(x)∈A;
③若f(x)∈A,则y=f(x)可为奇函数;
④若f(x)∈A,则对任意不等实数x1,x2,总有
| f(x1)-f(x2) |
| x1-x2 |
其中所有正确命题的序号是______.(填上所有正确命题的序号)
①令x≥y≥0,f2(x)-f2(y)=0而f(x+y)f(x-y)=1,∴①错误的;
②当f(x)=kx时,f2(x)-f2(y)=k2x2-k2y2=k(x-y)•k(x+y)=f(x+y)•f(x-y)成立,∴②正确.
③令x=y=0可得f(0)=0;再令x=0,有f2(0)-f2(y)=f(y)f(-y)即f(y)(f(y)+f(-y))=0,
则有f(y)=0或f(-y)=-f(y),因此f(x)为奇函数,∴③正确;
④如函数f(x)满足条件:
<0成立.则函数在定义域上是减函数,
由②知当y=kx时,满足条件,但当k>0时,函数y=kx为增函数,∴④不满足条件,故∴④错误.
故答案为:②③
②当f(x)=kx时,f2(x)-f2(y)=k2x2-k2y2=k(x-y)•k(x+y)=f(x+y)•f(x-y)成立,∴②正确.
③令x=y=0可得f(0)=0;再令x=0,有f2(0)-f2(y)=f(y)f(-y)即f(y)(f(y)+f(-y))=0,
则有f(y)=0或f(-y)=-f(y),因此f(x)为奇函数,∴③正确;
④如函数f(x)满足条件:
| f(x1)-f(x2) |
| x1-x2 |
由②知当y=kx时,满足条件,但当k>0时,函数y=kx为增函数,∴④不满足条件,故∴④错误.
故答案为:②③

练习册系列答案
相关题目
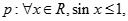 则
则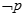 是( ).
是( ).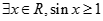
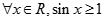
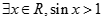
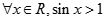
 ,命题
,命题 ,那么( )
,那么( ) 或
或 ”为假
”为假 或
或 ”为假
”为假 )x<(
)x<( )x;
)x; x>
x> x;
x; ,
, .则
.则 为
为 ,
,
 ,
, ,
,
 ,
,