题目内容
某网站用“10分制”调查一社区人们的幸福度.现从调查人群中随机抽取16名,以下茎叶图记录了他们的幸福度分数(以小数点前的一位数字为茎,小数点后的一位数字为叶):
(1)若幸福度不低于9.5分,则称该人的幸福度为“极幸福”,求从这16人随机选取3人,至多有1人是“极幸福”的概率;
(2)以这16人的样本数据来估计整个社区的总体数据,若从该社区(人数很多)任选3人,记 表示抽到“极幸福”的人数,求
表示抽到“极幸福”的人数,求 的分布列及数学期望.
的分布列及数学期望.
(1) ;(2)分布列详见解析,
;(2)分布列详见解析, .
.
解析试题分析:本题考查茎叶图的读法和期望及分布列问题,考查学生的分析能力和计算能力.第一问,至多有1人是“极幸福”,包含2种情况:有1人是“极幸福”,有0人是“极幸福”,这一问利用公式计算,较简单;第二问,对事件进行分析是本问的关键,先求出选1人为“极幸福”的概率 ,利用
,利用 ,利用二项分布计算出每种情况下的概率,这部分是关键,以下的分布列和期望都需要用这些数.
,利用二项分布计算出每种情况下的概率,这部分是关键,以下的分布列和期望都需要用这些数.
试题解析:(1)设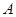 表示所取3人中有
表示所取3人中有 个人是“极幸福”,至多有1人是“极幸福”记为事件
个人是“极幸福”,至多有1人是“极幸福”记为事件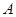 ,
,
所以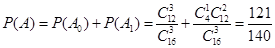 . (4分)
. (4分)
(2) 的可能取值为0,1,2,3.
的可能取值为0,1,2,3.
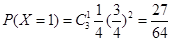
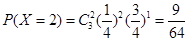

分布列为
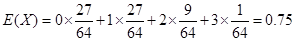
令解: 的可能取值为0,1,2,3.
的可能取值为0,1,2,3.
分布列为
所以 . (12分)
. (12分)
考点:1.茎叶图;2.分布列;3.二项分布.

练习册系列答案
相关题目
为了对某课题进行研究,用分层抽样方法从三所高校A,B,C的相关人员中,抽取若干人组成研究小组,有关数据见下表(单位:人)
| 高校 | 相关人数 | 抽取人数 |
| A | 18 |  |
| B | 36 | 2 |
| C | 54 | 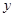 |
(1)求
 ,
,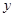 ;
;(2)若从高校B、C抽取的人中选2人作专题发言,
求这2人都来自高校C的概率.
 顶点
顶点 起跳,每步从一顶点跳到相邻的顶点.
起跳,每步从一顶点跳到相邻的顶点.
 的概率
的概率 ;
; 表示跳到过
表示跳到过 .
. ,甲、丙两人都回答错误的概率是
,甲、丙两人都回答错误的概率是 ,乙、丙两人都回答正确的概率是
,乙、丙两人都回答正确的概率是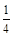 .
. 表示回答该题正确的人数,求
表示回答该题正确的人数,求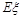 .
. 的概率分布列及期望.
的概率分布列及期望.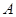 饮料,另外2杯为
饮料,另外2杯为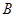 饮料,公司要求此员工一一品尝后,从5杯饮料中选出3杯
饮料,公司要求此员工一一品尝后,从5杯饮料中选出3杯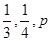 ,
, .
. 的值,
的值,