题目内容
一个袋中装有大小相同的球10个,其中红球8个,黑球2个,现从袋中有放回地取球,每次随机取1个. 求:
(Ⅰ)连续取两次都是红球的概率;
(Ⅱ)如果取出黑球,则取球终止,否则继续取球,直到取出黑球,取球次数最多不超过4次,求取球次数 的概率分布列及期望.
的概率分布列及期望.
(Ⅰ) ;(Ⅱ)见解析.
;(Ⅱ)见解析.
解析试题分析:(Ⅰ)利用分步原理可得概率为 ;(Ⅱ)根据题意得出
;(Ⅱ)根据题意得出 的可能取值为1,2,3,4,列出分布列计算期望.
的可能取值为1,2,3,4,列出分布列计算期望.
试题解析:(Ⅰ)连续取两次都是红球的概率 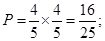 3分
3分
(Ⅱ) 的可能取值为1,2,3,4, . 4分
的可能取值为1,2,3,4, . 4分 ,
, ,
, ,
, . . 8分
. . 8分 的概率分布列为
的概率分布列为
10分
1 2 3 4 




E =1×
=1× +2×
+2× +3×
+3× +4×
+4× =
= . 12分
. 12分
考点:分步计数原理、离散型随机变量的分布列和数学期望.

练习册系列答案
相关题目
某市 、
、 、
、 、
、 四所中学报名参加某高校今年自主招生的学生人数如下表所示:
四所中学报名参加某高校今年自主招生的学生人数如下表所示:
| 中学 |  |  |  |  |
| 人数 |  |  |  |  |
 名参加问卷调查.
名参加问卷调查.(1)问
 、
、 、
、 、
、 四所中学各抽取多少名学生?
四所中学各抽取多少名学生?(2)从参加问卷调查的
 名学生中随机抽取两名学生,求这两名学生来自同一所中学的概率;
名学生中随机抽取两名学生,求这两名学生来自同一所中学的概率;(3)在参加问卷调查的
 名学生中,从来自
名学生中,从来自 、
、 两所中学的学生当中随机抽取两名学生,用
两所中学的学生当中随机抽取两名学生,用 表示抽得
表示抽得 中学的学生人数,求
中学的学生人数,求 的分布列.
的分布列. 甲,乙,丙三位学生独立地解同一道题,甲做对的概率为 ,乙,丙做对的概率分别为
,乙,丙做对的概率分别为 ,
, (
( >
> ),且三位学生是否做对相互独立.记
),且三位学生是否做对相互独立.记 为这三位学生中做对该题的人数,其分布列为:
为这三位学生中做对该题的人数,其分布列为:
 | 0 | 1 | 2 | 3 |
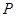 |  | 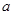 |  |  |
(Ⅱ)求
 ,
, 的值;
的值;(Ⅲ)求
 的数学期望.
的数学期望.  有三个选项,问题
有三个选项,问题 有四个选项,但都只有一个选项是正确的,正确回答问题
有四个选项,但都只有一个选项是正确的,正确回答问题 元,正确回答问题
元,正确回答问题 元,活动规定:参与者可任意选择回答问题的顺序,如果第一个问题回答正确,则继续答题,否则该参与者猜奖活动终止,假设一个参与者在回答问题前,对这两个问题都很陌生.
元,活动规定:参与者可任意选择回答问题的顺序,如果第一个问题回答正确,则继续答题,否则该参与者猜奖活动终止,假设一个参与者在回答问题前,对这两个问题都很陌生.

 只,其中有
只,其中有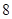 只合格品,
只合格品, 只次品。
只次品。 次,每次取一只灯泡,求
次,每次取一只灯泡,求 的分布列和数学期望.
的分布列和数学期望.
 表示抽到“极幸福”的人数,求
表示抽到“极幸福”的人数,求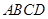 的边长为2,
的边长为2, 分别是边
分别是边 的中点.
的中点. ,求满足
,求满足 的概率;
的概率; 这八个点中,随机选取两个点,记这两个点之间的距离为
这八个点中,随机选取两个点,记这两个点之间的距离为 ,求随机变量
,求随机变量 .
.