题目内容
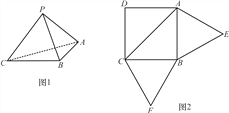
【题目】已知三棱锥![]() (如图
(如图![]() )的平面展开图(如图
)的平面展开图(如图![]() )中,四边形
)中,四边形![]() 为边长为
为边长为![]() 的正方形,
的正方形,![]() 和
和![]() 均为正三角形,在三棱锥
均为正三角形,在三棱锥![]() 中:
中:

(1)证明:平面![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
【答案】(1)见解析;(2)![]() .
.
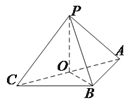
【解析】分析:(1)设AC的中点为O,连接BO,PO.推导出PO⊥AC,PO⊥OB,从而 PO⊥平面ABC,由此能证明平面PAC⊥平面ABC.
(2)由PO⊥平面ABC,OB⊥AC,建立空间直角坐标系,利用向量法能求出二面角A﹣PC﹣B的余弦值.
详解:(1)证明:
设![]() 的中点为
的中点为![]() ,连接
,连接![]() ,
,![]() .由题意得,
.由题意得,
![]() ,
,![]() ,
,![]() ,
,
因为在![]() 中,
中,![]() ,
,![]() 为
为![]() 的中点,
的中点,
所以![]() ,
,
因为在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,
所以![]() ,
,
因为![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() ,
,
因为![]() 平面
平面![]() ,
,
所以平面![]()
![]() 平面
平面![]() .
.
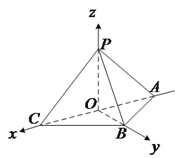
(2)解:由![]() 平面
平面![]() ,
,![]() ,如图建立空间直角坐标系,则
,如图建立空间直角坐标系,则
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
由![]() 平面
平面![]() ,故平面
,故平面![]() 的法向量为
的法向量为![]() ,
,
由![]() ,
,![]() ,
,
设平面![]() 的法向量为
的法向量为![]() ,则
,则
由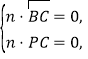 得:
得:![]()
令![]() ,得
,得![]() ,
,![]() ,即
,即![]() ,
,
![]() .
.
由二面角![]() 是锐二面角,
是锐二面角,
所以二面角![]() 的余弦值为
的余弦值为![]() .
.

练习册系列答案
 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
【题目】某机构为研究学生玩电脑游戏和对待作业量态度的关系,随机抽取了100名学生进行调查,所得数据如下表所示:
认为作业多 | 认为作业不多 | 总计 | |
喜欢玩电脑游戏 | 25 | 15 | 40 |
不喜欢玩电脑游戏 | 25 | 35 | 60 |
总计 | 50 | 50 | 100 |
(参考公式![]() ,可能用到数据:
,可能用到数据:![]() ,
,![]() ),参照以上公式和数据,得到的正确结论是( )
),参照以上公式和数据,得到的正确结论是( )
A. 有![]() 的把握认为喜欢玩电脑游戏与对待作业量的态度有关
的把握认为喜欢玩电脑游戏与对待作业量的态度有关
B. 有![]() 的把握认为喜欢玩电脑游戏与对待作业量的态度无关
的把握认为喜欢玩电脑游戏与对待作业量的态度无关
C. 有![]() 的把握认为喜欢玩电脑游戏与对待作业量的态度有关
的把握认为喜欢玩电脑游戏与对待作业量的态度有关
D. 有![]() 的把握认为喜欢玩电脑游戏与对待作业量的态度无关
的把握认为喜欢玩电脑游戏与对待作业量的态度无关