题目内容
2.定义在R上的函数f(x)满足f(1)=1,且对任意x∈R都有f′(x)<$\frac{1}{2}$,则不等式f(x)>$\frac{x+1}{2}$的解集为(-∞,1).分析 设g(x)=f(x)-$\frac{x+1}{2}$,求出g(1),求出g(x)的导函数,确定其单调性,由单调性列式求解.
解答 解:设g(x)=f(x)-$\frac{x+1}{2}$,g(1)=f(1)-$\frac{1+1}{2}$=0,
则g′(x)=f′(x)-$\frac{1}{2}$,
∵对任意x∈R,都有f′(x)<$\frac{1}{2}$,
∴g′(x)<0,即g(x)为实数集上的减函数.
不等式即为g(x)>0=g(1).
则x<1,
∴不等式的解集为(-∞,1).
故答案为:(-∞,1).
点评 本题考查了利用导数研究函数的单调性,考查了函数构造法,解答的关键是正确构造出辅助函数,是中档题.

练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目
12.执行如图的程序框图,若输入m的值为2,则输出的结果i=( )
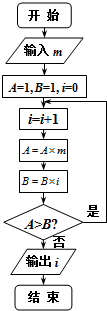

| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
13.散点图在回归分析过程中的作用是( )
| A. | 查找个体个数 | B. | 粗略判断变量是否线性相关 | ||
| C. | 探究个体分类 | D. | 比较个体数据大小关系 |
10.已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0),两个焦点分别为F1、F2,若在第一象限内双曲线上存在一点P,使得在△PF1F2中,∠PF1F2=30°,∠PF2F1=90°,则此双曲线的渐近线方程为( )
| A. | $y=±\frac{{\sqrt{2}}}{2}x$ | B. | $y=±\sqrt{2}x$ | C. | $y=±\sqrt{3}x$ | D. | y=±2x |
7.某校有6间不同的电脑室,每天晚上至少开放2间,求不同安排方案的种数,现有四位同学分别给出下列四个结果①$C_6^2$;②26-7;③$C_6^3+2C_6^4+C_6^5+C_6^6$,其中正确的结论是( )
| A. | ① | B. | ②与③ | C. | ①与② | D. | ①②③ |
14.设6件产品中有4件合格品2件不合格品,从中任意取2件,则其中至少一件是不合格品的概率为( )
| A. | 0.4 | B. | 0.5 | C. | 0.6 | D. | 0.7 |