题目内容
设p：x2-x-6≤0，q：x2-（2a+1）x+a（a+1）≤0，若p是q的必要不充分条件，求实数a的取值范围．
由x2-x-6≤0，得-2≤x≤3，即p：-2≤x≤3．
由x2-（2a+1）x+a（a+1）≤0，得（x-a）（x-a-1）≤0，
即：a≤x≤a+1．q：a≤x≤a+1．
要使p是q的必要不充分条件，
则
且等号不能同时取，
即
，
∴-2≤a≤2，
故a的取值范围是-2≤a≤2．
由x2-（2a+1）x+a（a+1）≤0，得（x-a）（x-a-1）≤0，
即：a≤x≤a+1．q：a≤x≤a+1．
要使p是q的必要不充分条件，
则
|
即
|
∴-2≤a≤2，
故a的取值范围是-2≤a≤2．
练习册系列答案
快捷英语周周练系列答案
相关题目
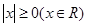”的否定是（ ）
.“
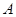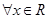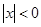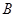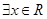，使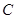
” 
. “
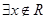，使
.“
，使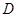
.“
”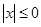