题目内容
“OA∥O1A1,OB∥O1B1”是“∠AOB=∠A1O1B1”的( )
| A.充要条件 | B.充分不必要条件 |
| C.必要不充分条件 | D.既不充分又不必要条件 |
在空间中,当“OA∥O1A1,OB∥O1B1”,则“∠AOB=∠A1O1B1”或“∠AOB=π-∠A1O1B1”,所以不成立.如图1.
同理当“∠AOB=∠A1O1B1”时,也无法得到OA∥O1A1,OB∥O1B1”,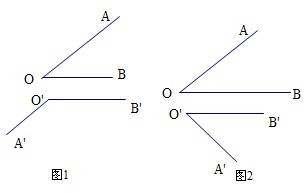 如图2.
如图2.
所以“OA∥O1A1,OB∥O1B1”是“∠AOB=∠A1O1B1”的既不充分又不必要条件.
故选D.
同理当“∠AOB=∠A1O1B1”时,也无法得到OA∥O1A1,OB∥O1B1”,
 如图2.
如图2.所以“OA∥O1A1,OB∥O1B1”是“∠AOB=∠A1O1B1”的既不充分又不必要条件.
故选D.

练习册系列答案
相关题目
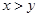 ,则
,则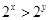 ”的否命题为假命题
”的否命题为假命题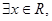 使得
使得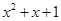
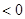 ”的否定为“
”的否定为“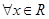 ,满足
,满足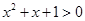 ”
”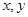 为实数,则“
为实数,则“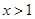 ”是“
”是“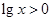 ”的充要条件
”的充要条件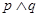 ”为假命题,则
”为假命题,则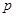 和
和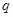 都是假命题
都是假命题