题目内容
20.复数z满足zi=2-i(i为虚数单位),则$\overline{z}$=( )| A. | 2-i | B. | 1+2i | C. | -1-2i | D. | -1+2i |
分析 把给出的等式变形,然后利用复数代数形式的乘除运算化简,再由共轭复数的概念得答案.
解答 解:由zi=2-i,得$z=\frac{2-i}{i}=\frac{(2-i)(-i)}{-{i}^{2}}=-1-2i$,
∴$\overline{z}=-1+2i$.
故选:D.
点评 本题考查复数代数形式的乘除运算,考查了共轭复数的概念,是基础题.

练习册系列答案
相关题目
12.某地一天的时间t(小时,0≤t≤24)时刻与对应温度T(度)的变化曲线近似满足函数T=Asin(ωt+φ)+B(ω>0,|φ|<π),某同学用“五点法”作此函数图象,在一天内的五个关键时刻与温度对应数据如下表:
(1)请写出上表中的t1,t2,并求函数T的解析式;
(2)若某天的温度T与时间t的关系恰好比上表对应关系延迟了1小时(即图象向右平移1个单位长度),在这一天的9点到16点,何时温度最低,最低温度是多少.
| t | 0 | t1 | 12 | t2 | 24 |
| ωt+φ | -$\frac{π}{2}$ | 0 | $\frac{π}{2}$ | π | $\frac{3π}{2}$ |
| T | 20 | 25 | 30 | 25 | 20 |
(2)若某天的温度T与时间t的关系恰好比上表对应关系延迟了1小时(即图象向右平移1个单位长度),在这一天的9点到16点,何时温度最低,最低温度是多少.
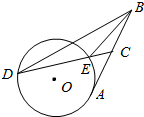 如图,AB为圆O的切线,A为切点,过线段AB上一点C作圆O的割线CED(E在C、D之间),且∠BEC=∠DBC,求证:BC=CA.
如图,AB为圆O的切线,A为切点,过线段AB上一点C作圆O的割线CED(E在C、D之间),且∠BEC=∠DBC,求证:BC=CA. 如图所示,AB是⊙O的直径,过圆上异于A、B的一点E作切线CD,交AB的延长线于点C,过A作AD⊥CD交圆于F,若CB=2,CE=4,则AD的长为$\frac{24}{5}$.
如图所示,AB是⊙O的直径,过圆上异于A、B的一点E作切线CD,交AB的延长线于点C,过A作AD⊥CD交圆于F,若CB=2,CE=4,则AD的长为$\frac{24}{5}$.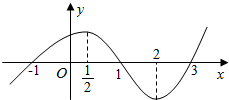 函数y=f(x)(x∈R)的图象如图所示,记y=f(x)的导函数为y=f′(x),则不等式x•f′(x)<0的解集为(-∞,0)∪($\frac{1}{2}$,2).
函数y=f(x)(x∈R)的图象如图所示,记y=f(x)的导函数为y=f′(x),则不等式x•f′(x)<0的解集为(-∞,0)∪($\frac{1}{2}$,2).