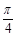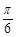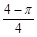题目内容
设随机变量 ~
~ ,又
,又 ,则
,则 和
和 的值分别是( )
的值分别是( )
A. 和 和 | B. 和 和 | C. 和 和 | D. 和 和 |
C
解析试题分析:因为随机变量 ~
~ ,所以
,所以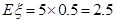 ,
,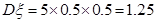 ,所以
,所以 =
= ,
, =
= 。
。
考点:二项分布;数学期望;方差。
点评:本题考查二项分布的性质和应用,解题时要注意二项分布期望公式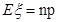 和方差公式Dξ=np(1-p)的灵活运用。
和方差公式Dξ=np(1-p)的灵活运用。

练习册系列答案
 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目
如图,边长为2的正方形中有一封闭曲线围成的阴影区域,在正方形中随机撒一粒豆子(假设它落在正方形区域内任何位置的机会均等),它落在阴影区域内的概率为 ,则阴影区域的面积为( )
,则阴影区域的面积为( )
A. | B. | C. | D.无法计算 |
若以连续掷两次骰子分别得到的点数 作为点
作为点 的坐标,则点
的坐标,则点 落在圆
落在圆 内的概率为( )
内的概率为( )
A. | B. | C. | D. |
如图,某人向圆内投镖,如果他每次都投入圆内,那么他投中正方形区域的概率为
A. | B. | C. | D. |
已知函数: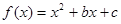 ,其中:
,其中: ,记函数
,记函数 满足条件:
满足条件: 为事件为
为事件为 ,则事件
,则事件 发生的概率为( )
发生的概率为( )
A. | B. | C. | D. |
离散型随机变量X的概率分布列如下:
则c等于( )
| A.0.01 | B.0.24 | C.0.1 | D.0.76 |




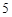 ,宽为
,宽为 ,在矩形内随机地撒
,在矩形内随机地撒 颗黄豆,数得落在阴影部分的黄豆数为
颗黄豆,数得落在阴影部分的黄豆数为 颗,由此我们可以估计出阴影部分的面积约( )
颗,由此我们可以估计出阴影部分的面积约( )




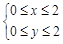 表示的平面区域为
表示的平面区域为 ,在区域
,在区域