题目内容
如图的矩形,长为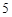 ,宽为
,宽为 ,在矩形内随机地撒
,在矩形内随机地撒 颗黄豆,数得落在阴影部分的黄豆数为
颗黄豆,数得落在阴影部分的黄豆数为 颗,由此我们可以估计出阴影部分的面积约( )
颗,由此我们可以估计出阴影部分的面积约( )
A. | B. | C. | D. |

C
解析试题分析:由已知中矩形的长为5,宽为2,我们易计算出矩形的面积,根据随机模拟实验的概念,我们易得阴影部分的面积与矩形面积的比例约为黄豆落在阴影区域中的频率,由此我们构造关于S阴影的方程,解方程即可求出阴影部分面积.
矩形的长为5,宽为2,则S矩形=10,那么可知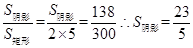 ,故答案为C
,故答案为C
考点:本题主要考查知识点是几何概型与随机模拟实验.
点评:利用阴影面积与矩形面积的比例约为黄豆落在阴影区域中的频率,构造关于S阴影的方程,是解答本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
设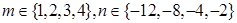 ,则函数
,则函数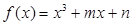 在区间
在区间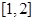 上有零点的概率是( )
上有零点的概率是( )
A.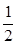 | B.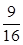 | C.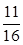 | D. |
口袋内装有大小相同的红球、白球和黑球,从中摸出一个球,摸出红球的概率是0.42,摸出白球的概率是0.28,则摸出黑球的概率是( )
| A.0.42 | B.0.28 | C.0.7 | D.0.3 |
设随机变量 ~
~ ,又
,又 ,则
,则 和
和 的值分别是( )
的值分别是( )
A. 和 和 | B. 和 和 | C. 和 和 | D. 和 和 |
下列说法一定正确的是( )
| A.一名篮球运动员,号称“百发百中”,若罚球三次,不会出现三投都不中的情况 |
B.一枚硬币掷一次得到正面的概率是 ,那么掷两次一定会出现一次正面的情况 ,那么掷两次一定会出现一次正面的情况 |
| C.如买彩票中奖的概率是万分之一,则买一万元的彩票一定会中奖一元 |
| D.随机事件发生的概率与试验次数无关 |
从装有红球和绿球的口袋内任取2个球(其中红球和绿球都多于2个),那么互斥而不对立的两个事件是( )
| A.至少有一个红球,至少有一个绿球 |
| B.恰有一个红球,恰有两个绿球 |
| C.至少有一个红球,都是红球 |
| D.至少有一个红球,都是绿球 |
 表示这5人中“三好学生”的人数,则下列概率中等于
表示这5人中“三好学生”的人数,则下列概率中等于 的是( )
的是( )




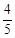


 和一件次品
和一件次品 的3件产品中每次任取1件,每次取出后放回,连续取两次,则取出的两件产品中恰有一件是次品的概率为( )
的3件产品中每次任取1件,每次取出后放回,连续取两次,则取出的两件产品中恰有一件是次品的概率为( )


