题目内容
若以连续掷两次骰子分别得到的点数 作为点
作为点 的坐标,则点
的坐标,则点 落在圆
落在圆 内的概率为( )
内的概率为( )
A. | B. | C. | D. |
A
解析试题分析:若以连续掷两次骰子分别得到的点数 作为点
作为点 的坐标,其所有的结果为:
的坐标,其所有的结果为: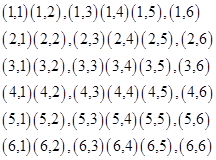 ,
,
共36种,满点 落在圆
落在圆 内的有
内的有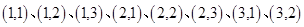 共8种,所有其概率为
共8种,所有其概率为 。
。
考点:古典概型。
点评:本题考查用列举法计算基本事件数及随机事件发生的概率,解题的关键是熟练运用分类列举的方法及事件的性质将所有的基本事件一一列举出来,运用公式求出概率,列举法求概率适合基本事件数不太多的概率求解问题,本题考查了分类的思想。

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案
相关题目
从装有2个红球和2个白球的口袋里任取2个球,那么互斥而不对立的两个事件是
| A.至少1个白球,都是白球 |
| B.至少1个白球,至少1个红球 |
| C.至少1个白球,都是红球 |
| D.恰好1个白球,恰好2个白球 |
口袋内装有大小相同的红球、白球和黑球,从中摸出一个球,摸出红球的概率是0.42,摸出白球的概率是0.28,则摸出黑球的概率是( )
| A.0.42 | B.0.28 | C.0.7 | D.0.3 |
设随机变量 ~
~ ,又
,又 ,则
,则 和
和 的值分别是( )
的值分别是( )
A. 和 和 | B. 和 和 | C. 和 和 | D. 和 和 |

 B.
B. C.
C. D.
D.


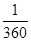


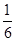



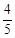


 (x>0)图象下方的区域(阴影部分),从D内随机取一个点M,则点M取自E内的概率为( )
(x>0)图象下方的区域(阴影部分),从D内随机取一个点M,则点M取自E内的概率为( )



