题目内容
已知函数: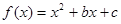 ,其中:
,其中: ,记函数
,记函数 满足条件:
满足条件: 为事件为
为事件为 ,则事件
,则事件 发生的概率为( )
发生的概率为( )
A. | B. | C. | D. |
B
解析试题分析:我们可以以b,c为横纵坐标建立坐标系,并把0≤b≤4,0≤c≤4所表示的区域表示出来,并将 ,代入函数f(x)=x2+bx+x转化为一个关于b、c的不等式,画出其表示的图形,计算面积后,代入几何概型公式,即可求解.
,代入函数f(x)=x2+bx+x转化为一个关于b、c的不等式,画出其表示的图形,计算面积后,代入几何概型公式,即可求解.
因为即4+2b+c≤12,4-2b+c≤4.以b,c为横纵坐标建立坐标系如图:
所以满足条件的概率为
.故选B
考点:本题主要考查了几何概型概率的计算的运用,
点评:解决该试题的关键是几何概型的概率估算公式中的“几何度量”,可以为线段长度、面积、体积等,而且这个“几何度量”只与“大小”有关,而与形状和位置无关.解决的步骤均为:求出满足条件A的基本事件对应的“几何度量”N(A),再求出总的基本事件对应的“几何度量”N,最后根据P= 求解.
求解.

练习册系列答案
相关题目
设随机变量 ~
~ ,又
,又 ,则
,则 和
和 的值分别是( )
的值分别是( )
A. 和 和 | B. 和 和 | C. 和 和 | D. 和 和 |
下列说法一定正确的是( )
| A.一名篮球运动员,号称“百发百中”,若罚球三次,不会出现三投都不中的情况 |
B.一枚硬币掷一次得到正面的概率是 ,那么掷两次一定会出现一次正面的情况 ,那么掷两次一定会出现一次正面的情况 |
| C.如买彩票中奖的概率是万分之一,则买一万元的彩票一定会中奖一元 |
| D.随机事件发生的概率与试验次数无关 |
在某一试验中事件A出现的概率为 ,则在
,则在 次试验中
次试验中 出现
出现 次的概率为( )
次的概率为( )
A.1- | B. |
C.1- | D. |


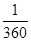


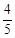


 和一件次品
和一件次品 的3件产品中每次任取1件,每次取出后放回,连续取两次,则取出的两件产品中恰有一件是次品的概率为( )
的3件产品中每次任取1件,每次取出后放回,连续取两次,则取出的两件产品中恰有一件是次品的概率为( )




 (x>0)图象下方的区域(阴影部分),从D内随机取一个点M,则点M取自E内的概率为( )
(x>0)图象下方的区域(阴影部分),从D内随机取一个点M,则点M取自E内的概率为( )



