题目内容
盒中装有形状,大小完全相同的5个球,其中红色球3个,黄色球2个,若从中随机取出2个球,已知其中一个为红色,则另一个为黄色的概率为
A. | B. | C. | D. |
C
解析试题分析:根据题意得:含有红色球的基本事件有9个,其中一红球、一黄球的基本事件有6个,由此结合古典概型的概率公式即可算出所求的概率.
解:记红色球分别为a、b、c,黄色球分别为d、e,
∵随机取出2个球,其中一个为红色,∴所有的基本事件为
(a,b),(a,c),(b,c),(a,d),(a,e),(b,d),(b,e),(c,d),(c,e)共9个
符合题意的基本事件为:(a,d),(a,e),(b,d),(b,e),(c,d),(c,e)共6个
因此,另一个为黄色的概率为:P=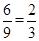 ,故选:C
,故选:C
考点:古典概型
点评:本题给出摸球事件,求在其中一个为红色的情况下,另一个为黄色的概率.着重考查了等可能事件的概率及其求法等知识,属于基础题.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
设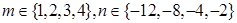 ,则函数
,则函数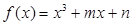 在区间
在区间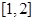 上有零点的概率是( )
上有零点的概率是( )
A.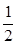 | B.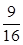 | C.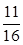 | D. |
设随机变量 ~
~ ,又
,又 ,则
,则 和
和 的值分别是( )
的值分别是( )
A. 和 和 | B. 和 和 | C. 和 和 | D. 和 和 |
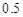 和
和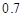 ,则两次射击中至少有一次命中目标的概率是( )
,则两次射击中至少有一次命中目标的概率是( )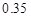
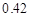
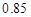
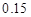
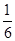
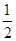



 B.
B. C.
C. D.
D.
 .质点P移动5次后位于点(2,3)的概率是( )
.质点P移动5次后位于点(2,3)的概率是( )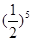
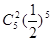
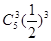
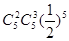
 的分布列如下表,随机变量
的分布列如下表,随机变量 ,则
,则 的值为( )
的值为( )
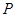


 C.
C.